Siguiente: Diferenciales y curvas Arriba: Diferenciación Anterior: Consideraciones heurísticas

Caso de variedades con bordes

Sean $M$, $N$ variedades con bordes de clase $C^k$ y $\varphi \colon M \to N$ una aplicación diferenciable en un punto $m \in M$.

En virtud del teorema 5.5.7 $\forall \, g \in {\cal D}(\varphi (m))$ la función compuesta $g \circ \varphi$ es diferenciable en el punto $m$, luego $g \circ \varphi \in {\cal D}(m)$ y tiene sentido operar sobre $g \circ \varphi$ por vectores $\vec u \in M_m$.

Esto sentado, se ve que tanto el enunciado como la demostración del teorema 5.5.7 conservan sin más su validez. La aplicación lineal, siempre notada $d \varphi (m)$ de $M_m$ en $N_{\varphi(m)}$ se define como allí. Se sigue llamando la DIFERENCIAL DE LA APLICACIÓN EN EL PUNTO DE LA VARIEDAD CON BORDE . Será, pues, razonable, como haremos, formular los resultados a continuación para variedades con bordes.

Definición 2.1   Sean $M, N$ variedades $C^k$ con borde y $\varphi \colon M \to N$ una aplicación diferenciable en un punto $m \in M$. El rango de la aplicación lineal $d \varphi(m) \colon M_m \to N_{\varphi (m)}$ se llama el RANGO DE LA APLICACIÓN EN EL PUNTO . Lo designaremos por $\mbox{\rm ran}_m \varphi$.

Observación 1

Sea $(U,x)$ un mapa admisible en un punto $m$ de una variedad con borde $M$ de clase $C^k$. En el enunciado del teorema 6.1.9 (generalización a variedades con borde del teorema 6.1.4) definimos un isomorfismo lineal $x_\ast (m)$ del espacio vectorial tangente $U_m \approx M_m$ sobre el espacio vectorial tangente $x(U)_{x(m)} \approx \left( {\mathbb{R}}^n \right)_{x(m)}$ por la fórmula:

$$\left( x_\ast (m) \vec u \right) \cdot g = \vec u \cdot (g \c... ...x) \quad \forall \, g \in {\cal D}_{x(U)} \left( x(m) \right)$$

Cotejando con la definición de la diferencial vemos que dicho isomorfismo $x_\ast (m)$ no es otro que la diferencial $dx(m)$ de la aplicación $x \colon U \to x(U)$ en el punto $m$. En particular:

$$\fbox{${\displaystyle \mbox{\rm ran}_m x = \mbox{\rm dim}_m M}$}$$

De aquí en adelante abandonaremos la notación provisional $x_\ast (m)$.

Observación 2 CARÁCTER LOCAL DE LA DIFERENCIAL

Sean $M, N$ variedades $C^k$ con bordes. Sean $m \in M$ y $G$ una vecindad abierta de $M$ en $m$. Supongamos $\varphi$ diferenciable en el punto $m$, equivalentemente (véase la observación después de la definición 5.5.8) la restricción $\varphi_G$ de $\varphi$ a $G$ diferenciable en el punto $m$. Se verifica:

$$\fbox{${\displaystyle d \varphi_G (m) = d \varphi(m)}$}$$

Demostración
Sea $\vec u$ un vector arbitrario de $M_m$, espacio vectorial identificado con $G_m$. Por la definición de la diferencial tenemos $\forall \, g \in {\cal D}(\varphi (m))$:

$$\left( d \varphi(m) \vec u \right) \cdot g = \vec u \cdot (g \circ \varphi) \quad {\rm y}$$ (1)

$$\left( d \varphi_G (m) \vec u \right) \cdot g = \vec u \cdot (g \circ \varphi_G)$$ (2)

Ya que $g \circ \varphi_G$ es una restricción de $g \circ \varphi$, por el principio de localización de vectores tangentes (tercer punto del teorema 6.1.2) los segundos miembros de las igualdades (1), (2) son iguales. De ahí:

$$d \varphi_G(m) = d \varphi(m)$$

$\quad\Box$

Teorema 2.2  

1. Si $M$ es una variedad con borde de clase $C^k$, vale $\forall \, m \in M$:
   
   $$\fbox{${\displaystyle d {\cal I}_M (m) = {\cal I}_{M_m}}$}$$
   
   

2. Sean $M,\ N,\ P$ variedades con bordes de clase $C^k$. Si $\varphi \colon M \to N$ es una aplicación diferenciable en un punto $m \in M$ y $\psi \colon N \to P$ es una aplicación diferenciable en el punto $\varphi (m) \in N$, vale la
   
   $$\fbox{${\displaystyle \begin{array}{c} \mbox{\rm {\sc Regla d... ...phi)(m) = d \psi (\varphi(m)) \circ d \varphi(m) \end{array}}$}$$
   
   

Demostración

1. El teorema 5.5.7 garantiza que la aplicación idéntica ${\cal I}_M$ es diferenciable en todo punto $m \in M$. $\forall \, \vec u \in M_m$ y $\forall \, f \in {\cal D}(m)$ tenemos:
   
   $$\left( d {\cal I}_m (m) \vec u \right) \cdot f = \vec u \cdot ( f \circ {\cal I}_M ) = \vec u \cdot f$$
   
   
   Luego $d {\cal I}_M (m) \vec u = \vec u\quad \forall \, \vec u \in M_m$, o sea $d {\cal I}_M (m) = {\cal I}_{M_m}$, como afirma el enunciado.
2. Adoptamos las notaciones del enunciado b). El teorema 5.5.7 garantiza la diferenciabilidad de la aplicación $\psi\circ \varphi$ en el punto $m$. Aplicando la definición de la diferencial obtenemos para cada vector $\vec u \in M_m$ y $\forall \, h \in {\cal D} \left( ( \psi \circ \varphi) (m) \right)$:
   $$\begin{eqnarray*} \left( d (\psi \circ \varphi) (m) \vec u \right) \cdot h &=& \... ...ft( d \psi (\varphi(m)) ( d \varphi(m) \vec u ) \right) \cdot h \end{eqnarray*}$$
   
   
   Luego $\left( d \psi (\varphi(m)) \circ d \varphi(m) \right) \vec u = d ( \psi \circ \varphi )(m) \vec u \quad \forall \, \vec u \in M_m$, o sea:
   
   $$d \psi (\varphi(m)) \circ d \varphi(m) = d (\psi \circ \varphi) (m)$$
   
   
   $\quad\Box$

Teorema 2.3   Sean $M, N$ variedades $C^k$ con bordes y $\varphi$ una biyección de $M$ sobre $N$. Se supone $\varphi$ diferenciable en un punto $m \in M$ y $\varphi^{-1}$ diferenciable en el punto $\varphi (m) \in N$. $d \varphi (m)$ es un isomorfismo lineal de $M_m$ sobre $N_{\varphi(m)}$ y $d \varphi^{-1}( \varphi(m))$ es el isomorfismo lineal de $N_{\varphi(m)}$ sobre $M_m$, inverso del precedente.

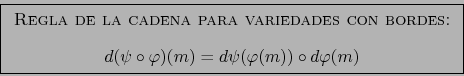
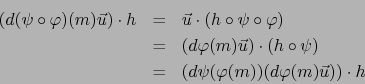
Demostración
Se verifican las relaciones:

$$\varphi^{-1} \circ \varphi = {\cal I}_M$$ (3)

$$\varphi \circ \varphi^{-1} = {\cal I}_N$$ (4)

Al tomar las diferenciales de ambos miembros de (3) en el punto $m \in M$ y los diferenciales en ambos miembros de (4) en el punto $\varphi (m) \in N$, hallamos en virtud de las dos partes del teorema 6.2.2:

$$d \varphi^{-1} ( \varphi(m)) \circ d \varphi(m) = {\cal I}_{M... ... \circ d \varphi^{-1}( \varphi(m)) = {\cal I}_{N_ {\varphi(m)}}$$

de donde la conclusión. $\quad\Box$

Observación
El teorema 6.2.3 se aplica en particular en todo punto $m \in M$ si $\varphi$ es un isomorfismo $C^k$ de $M$ sobre $N$. De ahí se sigue: Si $M, N$ son variedades $C^k$ con bordes, isomorfas $C^k$, son necesariamente de misma dimensión.

Siguiente: Diferenciales y curvas Arriba: Diferenciación Anterior: Consideraciones heurísticas