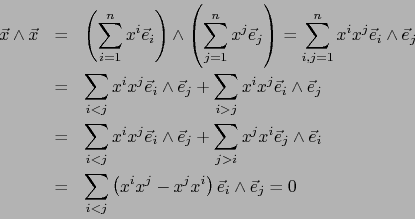Siguiente: Multivectores descomponibles
Arriba: Álgebra de Grassmann asociada
Anterior: Ley de conmutación
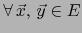 vale:
vale:
Al definir
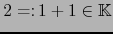 obtenemos de la última fórmula haciendo en
ella
obtenemos de la última fórmula haciendo en
ella
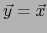 :
:
Si en el cuerpo  :
: 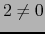 (o, como se dice,
(o, como se dice,  no es de característica 2) resulta
de ahí la regla:
no es de característica 2) resulta
de ahí la regla:
El teorema a continuación muestra que esta regla sigue válida en el caso general, o sea sin
ninguna hipótesis sobre la característica de  .
.
Demostración
Sea
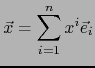 . Usando las relaciones
. Usando las relaciones
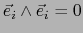 que sigue de la tabla
de multiplicación y
que sigue de la tabla
de multiplicación y
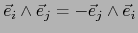 , caso particular del teorema 1.1.5, obtenemos:
, caso particular del teorema 1.1.5, obtenemos:

Guillermo M. Luna
2009-06-14
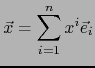 . Usando las relaciones
. Usando las relaciones
![]() que sigue de la tabla
de multiplicación y
que sigue de la tabla
de multiplicación y
![]() , caso particular del teorema 1.1.5, obtenemos:
, caso particular del teorema 1.1.5, obtenemos: