




Siguiente: Repaso de permutaciones
Arriba: Álgebra de Grassmann asociada
Anterior: Casos particulares
Definición 1.3
Un elemento de
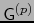 se llama -VECTOR DESCOMPONIBLE si puede expresarse en la forma
se llama -VECTOR DESCOMPONIBLE si puede expresarse en la forma
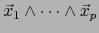 con
con
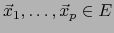 .
.
Notemos que la representación considerada está lejos de ser única. Si, por ejemplo, el vector 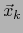 (
(
![$k \in [\![ 1,p ]\!]$](img240.png) ) se sustituye
por
) se sustituye
por
con
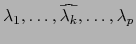 elementos arbitrarios
elementos arbitrarios![[*]](footnote.png) de
de  , no cambia el
producto
, no cambia el
producto
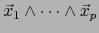 .
Del teorema 1.1.4 se sigue de inmediato que todo
.
Del teorema 1.1.4 se sigue de inmediato que todo  -vector puede expresarse como una suma de
-vector puede expresarse como una suma de  -vectores descomponibles. El ejemplo a continuación muestra que, sin
embargo, en general no todo
-vectores descomponibles. El ejemplo a continuación muestra que, sin
embargo, en general no todo  -vector es descomponible.
-vector es descomponible.
Ejemplo 1.1.
Suponemos 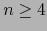 . Afirmamos que el bivector
. Afirmamos que el bivector
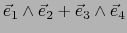 no es descomponible. Razonando
por contradicción supongamos que vale una relación:
no es descomponible. Razonando
por contradicción supongamos que vale una relación:
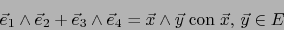 |
(21) |
Escribimos:
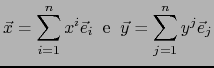 de donde:
de donde:
Llevando esto a (21) e igualando los coeficientes de
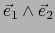 ,
,
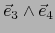 ,
,
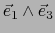 ,
,
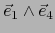 ,
,
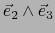 ,
,
 obtenemos:
obtenemos:
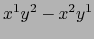 |
 |
 |
(22) |
 |
 |
 |
(23) |
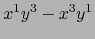 |
 |
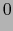 |
(24) |
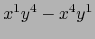 |
 |
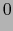 |
(25) |
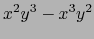 |
 |
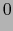 |
(26) |
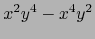 |
 |
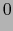 |
(27) |
De (22) se sigue que bien  o bien
o bien 
- Supongamos que
 .
.
Al poner
 obtenemos de (24):
obtenemos de (24):
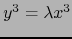 y de (25):
y de (25):
 . Estas
relaciones implican:
. Estas
relaciones implican:
en contradicción con (23).
- Supongamos
 . Ponemos
. Ponemos
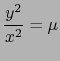 . Obtenemos de (26):
. Obtenemos de (26): 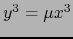 y de (6):
y de (6): 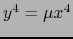 . Estas
relaciones implican de nuevo:
. Estas
relaciones implican de nuevo:
en contradicción con (23).
Las contradicciones obtenidas prueban que efectivamente el bivector considerado
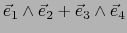 no es descomponible.
no es descomponible. 
Observación
Al suponer que la característica del cuerpo  no es 2, podemos probar lo anterior más simplemente. Supongamos
una relación
no es 2, podemos probar lo anterior más simplemente. Supongamos
una relación
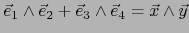 . Al cuadrar exteriormente
los dos miembros obtenemos de ahí:
. Al cuadrar exteriormente
los dos miembros obtenemos de ahí:
Por los teoremas 1.1.5 y 1.1.6 el segundo miembro de esta relación es cero. Vale pues:
 |
(28) |
Pero al desarrollar el primer miembro de (28) obtenemos, de nuevo con la ayuda de los teoremas 1.1.5 y 1.1.6:
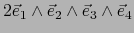 . La relación
(28) toma pues la forma:
. La relación
(28) toma pues la forma:
Si suponemos  , deducimos de ahí:
, deducimos de ahí:
Pero esto es un absurdo pues
![$\vec{e}_1 \wedge \vec{e}_2 \wedge \vec{e}_3 \wedge \vec{e}_4 = \overline{e}_{[\![ 1,4 ]\!]}$](img277.png) es uno de los
elementos de nuestra base privilegiada del álgebra G. De ahí la conclusión.
es uno de los
elementos de nuestra base privilegiada del álgebra G. De ahí la conclusión. 





Siguiente: Repaso de permutaciones
Arriba: Álgebra de Grassmann asociada
Anterior: Casos particulares
Guillermo M. Luna
2009-06-14
![[*]](footnote.png) de
de ![]() . Afirmamos que el bivector
. Afirmamos que el bivector
![]() no es descomponible. Razonando
por contradicción supongamos que vale una relación:
no es descomponible. Razonando
por contradicción supongamos que vale una relación:
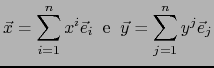 de donde:
de donde:
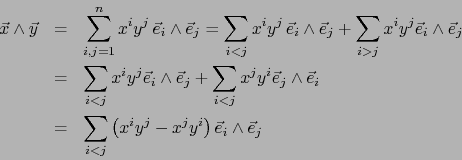
 obtenemos de (24):
obtenemos de (24):
![]() y de (25):
y de (25):
![]() . Estas
relaciones implican:
. Estas
relaciones implican:
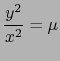 . Obtenemos de (26):
. Obtenemos de (26): ![]() no es 2, podemos probar lo anterior más simplemente. Supongamos
una relación
no es 2, podemos probar lo anterior más simplemente. Supongamos
una relación
![]() . Al cuadrar exteriormente
los dos miembros obtenemos de ahí:
. Al cuadrar exteriormente
los dos miembros obtenemos de ahí: