




Siguiente: Dualidad en álgebra exterior
Arriba: Repaso de dualidad
Anterior: Anuladores
Lema 2.1
Sea  un espacio vectorial de dimensión finita. Sea
un espacio vectorial de dimensión finita. Sea 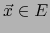 tal
que
tal
que
 . Entonces
. Entonces 
Demostración
Sea
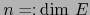 .
La hipótesis significa que
.
La hipótesis significa que
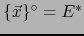 . Por el teorema 2.2.8, esto equivale
. Por el teorema 2.2.8, esto equivale
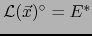 , o sea:
, o sea:
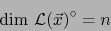 |
(13) |
Pero si fuese
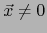 , sería
, sería
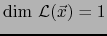 , de donde por el teorema 2.2.8,
, de donde por el teorema 2.2.8,
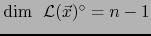 en contradicción con (13). Esta contradicción demuestra el lema.
en contradicción con (13). Esta contradicción demuestra el lema.

Corolario 2.2
Sea  un espacio vectorial de dimensión finita. Sean
un espacio vectorial de dimensión finita. Sean
 tales que:
tales que:
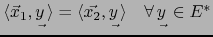 . Entonces
. Entonces
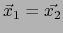 .
.
Teorema 2.10
Sea  un espacio vectorial. La aplicación
un espacio vectorial. La aplicación
 es una aplicación lineal inyectiva del espacio vectorial
es una aplicación lineal inyectiva del espacio vectorial  en su espacio
bidual
en su espacio
bidual 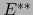 . Si
. Si  es de dimensión finita, dicha aplicación es
un isomorfismo lineal (canónico) de
es de dimensión finita, dicha aplicación es
un isomorfismo lineal (canónico) de  sobre
sobre 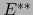 .
.
Demostración
- Sean
 ,
,
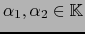 .
Por definición de
.
Por definición de 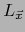 se verifica
se verifica
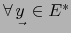 :
:
De donde al quitar el argumento
 :
:
 |
(14) |
Esto prueba que la aplicación
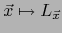 es una aplicación lineal de
es una aplicación lineal de  en
en 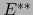 .
.
- Supongamos ahora que
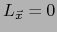 . Vale, pues,
. Vale, pues,
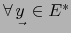 :
:
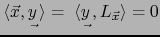 . Se sigue de ahí por el lema 2.2.1 que
. Se sigue de ahí por el lema 2.2.1 que  . Con esto viene probado que la aplicación lineal
. Con esto viene probado que la aplicación lineal
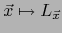 de
de  en
en 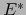 es inyectiva.
es inyectiva.
- Supongamos finalmente que
 es de dimensión finita. Por el inciso
b) y la consecuencia del teorema 2.2.1 el rango de la aplicación
es de dimensión finita. Por el inciso
b) y la consecuencia del teorema 2.2.1 el rango de la aplicación
 es
es
 . Así pues dicha aplicación es también superyectiva.
. Así pues dicha aplicación es también superyectiva.

Convenio
Si  es un espacio vectorial de dimensión finita, convenimos en identificar su bidual
es un espacio vectorial de dimensión finita, convenimos en identificar su bidual 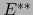 con el propio
con el propio  mediante el isomorfismo canónico del teorema 2.16. Vale decir: Todo operador
mediante el isomorfismo canónico del teorema 2.16. Vale decir: Todo operador
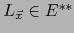 se identificará con
se identificará con 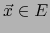 . Escribiremos
. Escribiremos 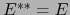 .
Sin embargo, cuando esto contribuya a la claridad usaremos notaciones dobles:
.
Sin embargo, cuando esto contribuya a la claridad usaremos notaciones dobles: 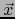 y
y 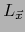 ;
;
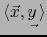 y
y
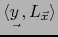 .
.
Demostración
 vale:
vale:
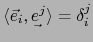 . Estas relaciones equivalen a:
. Estas relaciones equivalen a:
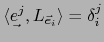 , de donde se ve que
, de donde se ve que
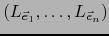 es la base de
es la base de 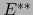 dual de la base
dual de la base
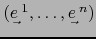 de
de 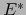 . En el lenguaje de nuestra identificación esto dice
que, efectivamente, la base
. En el lenguaje de nuestra identificación esto dice
que, efectivamente, la base
 de
de  es la base dual de la base
es la base dual de la base
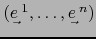 de
de 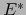 .
.

Observación
Sean  un espacio vectorial de dimensión finita y
un espacio vectorial de dimensión finita y 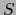 un subconjunto de
un subconjunto de 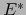 . El anulador
. El anulador 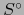 es un subespacio de
es un subespacio de 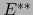 . Mediante nuestro convenio se identifica con un subespacio de
. Mediante nuestro convenio se identifica con un subespacio de  .
Explícitamente:
.
Explícitamente:
Las propiedades ya establecidas de anuladores siguen evidentemente válidas. A saber:
-
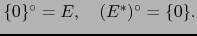
- Si
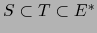 vale:
vale:
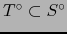 .
.
-

- Para todo subespacio
 de
de 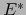 vale:
vale:
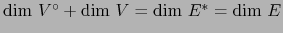 .
.
Teorema 2.12
Sea  un espacio vectorial de dimensión finita. Para todo subespacio
un espacio vectorial de dimensión finita. Para todo subespacio  de
de  se cumple:
se cumple:
Demostración
Pongamos
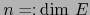 . Sea
. Sea 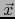 un elemento arbitrario de
un elemento arbitrario de  .
.
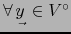 vale
vale
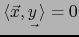 , luego
, luego
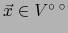 . Esto prueba que:
. Esto prueba que:
 |
(15) |
Pero también:
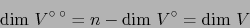 |
(16) |
De (15) y (16) se sigue
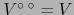 .
.

Corolario 2.3
Sea  un espacio vectorial de dimensión finita. Para todo subconjunto
un espacio vectorial de dimensión finita. Para todo subconjunto 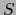 de
de  se cumple:
se cumple:
Teorema 2.13
Sea  un espacio vectorial de dimensión finita. Designemos por
un espacio vectorial de dimensión finita. Designemos por
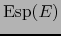 el conjunto de todos los subespacio de
el conjunto de todos los subespacio de  . La aplicación
. La aplicación
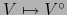 es una biyección de
es una biyección de
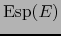 sobre
sobre
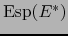 . La biyección inversa es la aplicación
. La biyección inversa es la aplicación
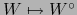 de
de
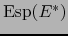 en
en
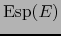 .
.
Demostración
Para más claridad, designemos por 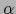 la aplicación
la aplicación
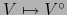 de
de
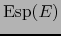 en
en
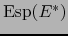 y por
y por  la aplicación
la aplicación
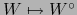 de
de
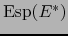 en
en
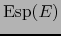 . Por el teorema 2.2.12 tenemos:
. Por el teorema 2.2.12 tenemos:
![\begin{displaymath}
\beta \circ \alpha = \left[\mbox{identidad de } \mbox{\rm Esp}(E)\right]
\end{displaymath}](img1550.png) |
(17) |
Intercambiando los papeles de 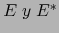 obtenemos también:
obtenemos también:
![\begin{displaymath}
\alpha \circ \beta = \left[\mbox{identidad de } \mbox{\rm Esp}(E^*)\right]
\end{displaymath}](img1552.png) |
(18) |
De las relaciones (17) y (18) se sigue sin más que
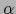 es una biyección de
es una biyección de
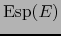 sobre
sobre
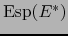 y
y  es la biyección inversa.
es la biyección inversa.






Siguiente: Dualidad en álgebra exterior
Arriba: Repaso de dualidad
Anterior: Anuladores
Guillermo M. Luna
2009-06-14
![]() sea
sea ![]() la aplicación de
la aplicación de ![]() en
en ![]() dada por:
dada por:
![]() sea
sea ![]() la aplicación de
la aplicación de ![]() en
en ![]() dada por:
dada por:
![]() .
La hipótesis significa que
.
La hipótesis significa que
![]() . Por el teorema 2.2.8, esto equivale
. Por el teorema 2.2.8, esto equivale
![]() , o sea:
, o sea:
![]() es un espacio vectorial de dimensión finita, convenimos en identificar su bidual
es un espacio vectorial de dimensión finita, convenimos en identificar su bidual ![]() con el propio
con el propio ![]() mediante el isomorfismo canónico del teorema 2.16. Vale decir: Todo operador
mediante el isomorfismo canónico del teorema 2.16. Vale decir: Todo operador
![]() se identificará con
se identificará con ![]() . Escribiremos
. Escribiremos ![]() .
Sin embargo, cuando esto contribuya a la claridad usaremos notaciones dobles:
.
Sin embargo, cuando esto contribuya a la claridad usaremos notaciones dobles: ![]() y
y ![]() ;
;
![]() y
y
![]() .
.
![]() con
con ![]() , la base
, la base
![]() llega a ser la base dual de la base
llega a ser la base dual de la base
![]() de
de ![]() .
.
![]() vale:
vale:
![]() . Estas relaciones equivalen a:
. Estas relaciones equivalen a:
![]() , de donde se ve que
, de donde se ve que
![]() es la base de
es la base de ![]() dual de la base
dual de la base
![]() de
de ![]() . En el lenguaje de nuestra identificación esto dice
que, efectivamente, la base
. En el lenguaje de nuestra identificación esto dice
que, efectivamente, la base
![]() de
de ![]() es la base dual de la base
es la base dual de la base
![]() de
de ![]() .
.
![]()
![]() un espacio vectorial de dimensión finita y
un espacio vectorial de dimensión finita y ![]() un subconjunto de
un subconjunto de ![]() . El anulador
. El anulador ![]() es un subespacio de
es un subespacio de ![]() . Mediante nuestro convenio se identifica con un subespacio de
. Mediante nuestro convenio se identifica con un subespacio de ![]() .
Explícitamente:
.
Explícitamente:
![]() . Sea
. Sea ![]() un elemento arbitrario de
un elemento arbitrario de ![]() .
.
![]() vale
vale
![]() , luego
, luego
![]() . Esto prueba que:
. Esto prueba que:
![]() la aplicación
la aplicación
![]() de
de
![]() en
en
![]() y por
y por ![]() la aplicación
la aplicación
![]() de
de
![]() en
en
![]() . Por el teorema 2.2.12 tenemos:
. Por el teorema 2.2.12 tenemos: