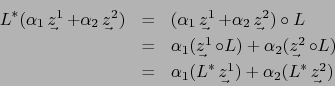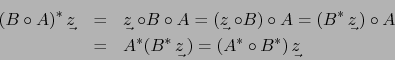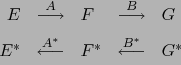Siguiente: Matriz de la aplicación
Arriba: Aplicaciones multilineales alternadas. Formas
Anterior: Aplicaciones multilineales alternadas
La teoría de espacios duales figura como parte de cualquier curso de
álgebra lineal. El sucinto repaso a continuación sirve, antes que todo,
para fijar terminología y notaciones.
Los elementos de  que, como antes, llamaremos VECTORES, los seguiremos designando por letras con flechas encima. Las formas lineales, elementos de
que, como antes, llamaremos VECTORES, los seguiremos designando por letras con flechas encima. Las formas lineales, elementos de 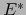 que también llamaremos COVECTORES, los designaremos por letras con flechas abajo.
que también llamaremos COVECTORES, los designaremos por letras con flechas abajo.
Si
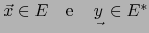 designaremos por el símbolo
designaremos por el símbolo
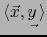 más bien que por
más bien que por
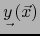 el escalar, valor de la forma lineal
el escalar, valor de la forma lineal
 sobre el vector
sobre el vector 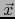 .
.
Rigen las reglas:
En otras palabras, la aplicación
 es una aplicación
bilineal de
es una aplicación
bilineal de 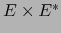 en
en
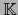 .
.
En efecto, la primera regla expresa meramente el hecho de que
 es una aplicación lineal. La segunda regla es solamente la definición de las operaciones en
es una aplicación lineal. La segunda regla es solamente la definición de las operaciones en
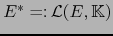 .
.
Estas relaciones caracterizan al covector
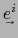 , pues una aplicación lineal del espacio vectorial
, pues una aplicación lineal del espacio vectorial  , en cualquier otro, está únicamente determinada por sus valores sobre una base de
, en cualquier otro, está únicamente determinada por sus valores sobre una base de  .
.
Demostración
- Supongamos una relación lineal
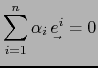 .
.
Evaluando ambos miembros de esta relación sobre un vector  obtenemos, en virtud de la relación (1):
obtenemos, en virtud de la relación (1):
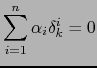 o sea
o sea 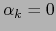 .
Esto es válido
.
Esto es válido
 . Luego la familia
. Luego la familia
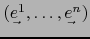 es linealmente independiente en
es linealmente independiente en
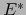 .
.
- Sea
 un covector, elemento de
un covector, elemento de 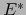 , arbitrario. Para un vector arbitrario
, arbitrario. Para un vector arbitrario
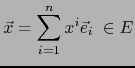 obtenemos:
obtenemos:
de ahí que (al quitar el argumento 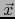 ):
):
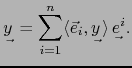 La última relación prueba que la familia
La última relación prueba que la familia
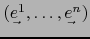 engendra el espacio vectorial
engendra el espacio vectorial 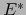 .
.
De a) y b) se sigue que
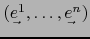 es una base de
es una base de 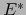 .
.

Para referencia destacamos la relación siguiente utilizada en la demostración precedente:
Consecuencia del teorema 2.2.1. Si  es un espacio vectorial de dimensión finita, lo es también
es un espacio vectorial de dimensión finita, lo es también 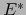 y se verifica:
y se verifica:
Observación
Sean  un espacio vectorial de dimensión finita provisto de una base
un espacio vectorial de dimensión finita provisto de una base
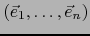 y
y 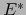 su espacio dual provisto de la base
su espacio dual provisto de la base
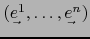 dual de la anterior.
dual de la anterior.
Sean 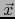 un vector arbitrario en
un vector arbitrario en  e
e
 un covector arbitrario en
un covector arbitrario en 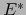 . Podemos escribir de manera única:
. Podemos escribir de manera única:
Afirmamos que entonces:
En efecto, usando la bilinealidad de la aplicación
 obtenemos:
obtenemos:

La aplicación
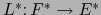 se llama la APLICACIÓN DUAL de la aplicación lineal
se llama la APLICACIÓN DUAL de la aplicación lineal
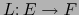 .
.
Observación
La definición de 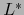 equivale patentemente a la regla:
equivale patentemente a la regla:
Teorema 2.2
- Con las notaciones de la definición 2.2.3,
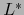 es una aplicación lineal de
es una aplicación lineal de 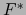 en
en 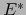 .
.
- La aplicación
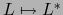 es una aplicación lineal del espacio vectorial
es una aplicación lineal del espacio vectorial 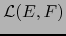 en el espacio vectorial
en el espacio vectorial
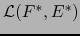 .
.
Demostración
-
 vale:
vale:
probando la afirmación a).
-
 vale:
vale:
O sea, quitando el argumento
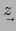 .
.

Teorema 2.3
- Si
 es un espacio vectorial, vale:
es un espacio vectorial, vale:
- Si
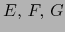 son espacios vectoriales y
son espacios vectoriales y
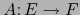 ,
,
 aplicaciones lineales, vale:
aplicaciones lineales, vale:
Demostración
-
 vale:
vale:
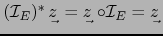 ; de ahí que
; de ahí que
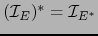 , probando la afirmación a).
, probando la afirmación a).
-
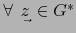 vale:
vale:
De ahí que:
 .
.

Note los diagramas:
con la inversión de las flechas en el segundo.
Teorema 2.4
Sean 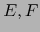 espacios vectoriales y
espacios vectoriales y  una aplicación lineal de
una aplicación lineal de  en
en  .
.
- Si
 es inyectiva,
es inyectiva, 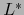 es una aplicación superyectiva de
es una aplicación superyectiva de 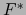 sobre
sobre 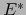 .
.
- Si
 es superyectiva,
es superyectiva, 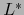 es una aplicación inyectiva de
es una aplicación inyectiva de 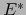 en
en 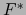 .
.
Demostración
- Supongamos
 inyectiva. Por el teorema 1.21 existe una aplicación
lineal
inyectiva. Por el teorema 1.21 existe una aplicación
lineal  de
de  en
en  tal que:
tal que:
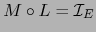 .
Tomando las aplicaciones duales de ambos miembros y aplicando el teorema 2.2.3
obtenemos de ahí:
.
Tomando las aplicaciones duales de ambos miembros y aplicando el teorema 2.2.3
obtenemos de ahí:
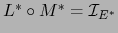 .
En virtud del teorema 1.4.4, esta relación entraña que
.
En virtud del teorema 1.4.4, esta relación entraña que 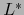 es superyectiva
es superyectiva
- Supongamos
 superyectiva. Por el teorema 1.22 existe una aplicación lineal
superyectiva. Por el teorema 1.22 existe una aplicación lineal
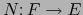 tal que:
tal que:
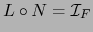 .
Tomando las aplicaciones duales de ambos miembros y aplicando el teorema 2.2.3 conseguimos de ahí:
.
Tomando las aplicaciones duales de ambos miembros y aplicando el teorema 2.2.3 conseguimos de ahí:
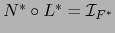 .
En virtud del teorema 1.4.3, esta relación entraña que
.
En virtud del teorema 1.4.3, esta relación entraña que 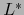 es inyectiva.
es inyectiva.

Corolario 2.1
Si  es un isomorfismo lineal de un espacio vectorial
es un isomorfismo lineal de un espacio vectorial  sobre un espacio vectorial
sobre un espacio vectorial  ,
, 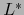 es un isomorfismo lineal de
es un isomorfismo lineal de 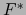 sobre
sobre 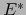 .
.
Teorema 2.5
Si  es un isomorfismo lineal de un espacio vectorial
es un isomorfismo lineal de un espacio vectorial  sobre un espacio
vectorial
sobre un espacio
vectorial  se verifica:
se verifica:
Demostración
Se cumplen la relaciones:
Al tomar las aplicaciones duales de ambos miembros de (2) y (3) y aplicar el teorema 2.2.3 conseguimos:
Las relaciones (4) y (5) prueban de nuevo que 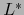 es un isomorfismo de
es un isomorfismo de 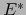 sobre
sobre 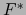 y
y
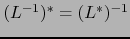 .
.

Subsections





Siguiente: Matriz de la aplicación
Arriba: Aplicaciones multilineales alternadas. Formas
Anterior: Aplicaciones multilineales alternadas
Guillermo M. Luna
2009-06-14
![]() que, como antes, llamaremos VECTORES, los seguiremos designando por letras con flechas encima. Las formas lineales, elementos de
que, como antes, llamaremos VECTORES, los seguiremos designando por letras con flechas encima. Las formas lineales, elementos de ![]() que también llamaremos COVECTORES, los designaremos por letras con flechas abajo.
que también llamaremos COVECTORES, los designaremos por letras con flechas abajo.
![]() designaremos por el símbolo
designaremos por el símbolo
![]() más bien que por
más bien que por
![]() el escalar, valor de la forma lineal
el escalar, valor de la forma lineal
![]() sobre el vector
sobre el vector ![]() .
.
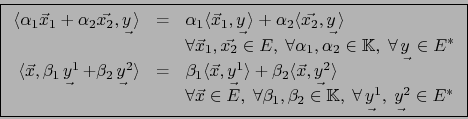
![]() es una aplicación
bilineal de
es una aplicación
bilineal de ![]() en
en
![]() .
.
![]() es una aplicación lineal. La segunda regla es solamente la definición de las operaciones en
es una aplicación lineal. La segunda regla es solamente la definición de las operaciones en
![]() .
.
![]() vale:
vale:
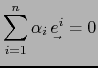 .
.
![]() obtenemos, en virtud de la relación (1):
obtenemos, en virtud de la relación (1):
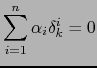 o sea
o sea ![]() .
Esto es válido
.
Esto es válido
![]() . Luego la familia
. Luego la familia
![]() es linealmente independiente en
es linealmente independiente en
![]() .
.
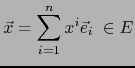 obtenemos:
obtenemos:
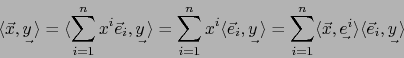
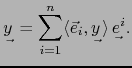 La última relación prueba que la familia
La última relación prueba que la familia

![]() es un espacio vectorial de dimensión finita, lo es también
es un espacio vectorial de dimensión finita, lo es también ![]() y se verifica:
y se verifica:
![]() un espacio vectorial de dimensión finita provisto de una base
un espacio vectorial de dimensión finita provisto de una base
![]() y
y ![]() su espacio dual provisto de la base
su espacio dual provisto de la base
![]() dual de la anterior.
dual de la anterior.
![]() un vector arbitrario en
un vector arbitrario en ![]() e
e
![]() un covector arbitrario en
un covector arbitrario en ![]() . Podemos escribir de manera única:
. Podemos escribir de manera única:

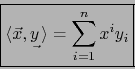
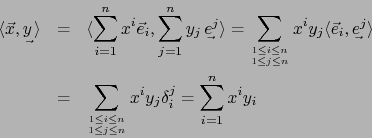
![]() equivale patentemente a la regla:
equivale patentemente a la regla: