Sea ![]() un espacio vectorial de dimensión finita. En esta sección,
además del álgebra exterior
un espacio vectorial de dimensión finita. En esta sección,
además del álgebra exterior ![]() sobre
sobre ![]() consideraremos el
álgebra exterior
consideraremos el
álgebra exterior ![]() sobre el dual
sobre el dual ![]() de
de ![]() . Por brevedad
la llamaremos ´ALGEBRA EXTERIOR DUAL SOBRE
. Por brevedad
la llamaremos ´ALGEBRA EXTERIOR DUAL SOBRE ![]() . Los elementos de
. Los elementos de ![]() se designarán por letras subrayadas.
se designarán por letras subrayadas.
A toda base
![]() de
de ![]() le asociamos la base
le asociamos la base
![]() del espacio
del espacio
![]() , dual de la
anterior. Si
, dual de la
anterior. Si
![]() , con
, con
![]() ,
,
![]() , ponemos:
, ponemos:
Los elementos del subespacio
Una vez hecha esta identificación se tendrá la fórmula:
Demostración
Debido al teorema 1.4.15, el determinante de una matriz
Llevando esta relación a (3), conseguimos:
b) Procedemos a probar que la aplicación lineal
Sea
Sean
La aplicación lineal
Convenimos en usar el isomorfismo
Observaciones
A) Debido a la identificación
B) La fórmula:
Pero todo elemento
C) Usando las bases
Por contraste con la fórmula (8), la fórmula (9) suministra explícitamente
el valor de cualquier
Sin embargo, comparada con (8), la fórmula (9) sufre la desventaja de no ser ``intrínseca'', pues exige el uso de bases y
componentes.
Una aplicación
Una fórmula para el determinante del producto de una matriz
Sean
Vamos a obtener una interesante fórmula para el determinante de esta
matriz
Sea
Consideramos los
Podemos, pues, escribir:
De ahí se sigue, por la fórmula (9) de la precedente
observación c):
Nota
![]() de
de ![]() (elementos
homogéneos de grado
(elementos
homogéneos de grado ![]() de
de ![]() ) se llaman -COVECTORES o FORMAS EXTERIORES de grado
) se llaman -COVECTORES o FORMAS EXTERIORES de grado ![]() sobre
sobre ![]() . Con las notaciones de arriba, la familia
. Con las notaciones de arriba, la familia
![]() constituye una base de
constituye una base de
![]() , la BASE DEL SUBESPACIO
, la BASE DEL SUBESPACIO ![]() de
de ![]() . Así pues, todo
. Así pues, todo ![]() -covector
-covector ![]() sobre
sobre ![]() se expresa únicamente en la forma:
se expresa únicamente en la forma:

He aquí el teorema principal de la sección:
![]() un espacio vectorial de dimensión finita
un espacio vectorial de dimensión finita ![]() .
.
![]() existe un isomorfismo lineal canónico del espacio vectorial
existe un isomorfismo lineal canónico del espacio vectorial
![]() (la
(la ![]() -ésima potencia exterior de
-ésima potencia exterior de ![]() ) sobre el espacio vectorial
) sobre el espacio vectorial
![]() (dual del espacio vectorial
(dual del espacio vectorial
![]() ) que permite identificar estos dos espacios vectoriales.
) que permite identificar estos dos espacios vectoriales.
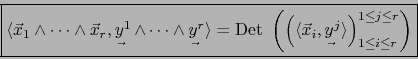
![]() .
.
![]() una base arbitraria de
una base arbitraria de ![]() y
y
![]() ,
,
![]() las bases de sendos espacios vectoriales
las bases de sendos espacios vectoriales
![]() y de
y de
![]() asociadas a ésta. Hecha la identificación mencionada, la base
asociadas a ésta. Hecha la identificación mencionada, la base
![]() de
de
![]() llega a ser la base dual de la base
llega a ser la base dual de la base
![]() de
de
![]() .
.
a) Fijemos por el momento un ![]() -uplo
-uplo
![]() de covectores, elementos de
de covectores, elementos de ![]() . Definamos una aplicación
. Definamos una aplicación
![]() de
de ![]() en
en ![]() por la fórmula:
por la fórmula:
Puesto que el determinante de una matriz cuadrada ![]() es una función
es una función ![]() -lineal alternada de las columnas de dicha matriz (consideradas como vectores en
-lineal alternada de las columnas de dicha matriz (consideradas como vectores en
![]() ) se sigue de la definición (2) que:
) se sigue de la definición (2) que:
![]()
Apliquemos la propiedad universal de la terna
![]() . Por la mencionada propiedad universal, existe una única aplicación
. Por la mencionada propiedad universal, existe una única aplicación
![]() en el espacio
en el espacio
![]() que hace conmutativo el diagrama:
que hace conmutativo el diagrama:
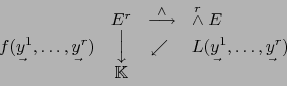
es decir:

Llevando esta relación a (2) obtenemos:
``Liberemos'' ahora
![]() y estudiemos la aplicación:
y estudiemos la aplicación:
![]()
de ![]() en
en
![]() .
.
![]() es también una función
es también una función ![]() -lineal alternada de las filas de dicha matriz (consideradas como vectores en
-lineal alternada de las filas de dicha matriz (consideradas como vectores en
![]() ). En vista de esto, se desprende fácilmente de la relación (3) que
). En vista de esto, se desprende fácilmente de la relación (3) que
![]() . Apliquemos la propiedad universal de la terna
. Apliquemos la propiedad universal de la terna
![]() . En virtud de ésta, existe una aplicación lineal única
. En virtud de ésta, existe una aplicación lineal única ![]() de
de
![]() en
en
![]() que hace conmutativo el diagrama:
que hace conmutativo el diagrama:
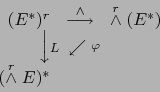
Vale decir:
![]() .
.
![]() es un isomorfismo lineal.
es un isomorfismo lineal.
![]() una base arbitraria de
una base arbitraria de ![]() . Usamos las bases
. Usamos las bases
![]() y
y
![]() asociados a ésta, en sendos espacios
asociados a ésta, en sendos espacios
![]() y
y
![]() .
.
![]() partes de
partes de
![]() de cardinalidad
de cardinalidad ![]() ; explícitamente:
; explícitamente:
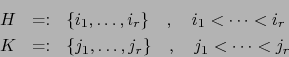
Tomemos en (3):
![]() para
para
![]() e
e
![]() para
para
![]() . Obtenemos de (3):
. Obtenemos de (3):
Ahora bien, por el lema 2.1.1, el último miembro de (4) es
![]() .
La relación (4) se convierte, pues, en:
.
La relación (4) se convierte, pues, en:
La relación (6) prueba que la familia
![]() es la base del dual
es la base del dual
![]() , dual de la base
, dual de la base
![]() del espacio vectorial
del espacio vectorial
![]() .
.
![]() transforma pues la base
transforma pues la base
![]() de
de
![]() en una base de
en una base de
![]() ; por lo tanto, es un isomorfismo del espacio vectorial
; por lo tanto, es un isomorfismo del espacio vectorial
![]() sobre el espacio
sobre el espacio
![]() dual de
dual de
![]() . Dicho isomorfismo es ``canónico'', pues su definición no exige ninguna elección de bases.
. Dicho isomorfismo es ``canónico'', pues su definición no exige ninguna elección de bases.
![]() como ``identificación''. Escribimos, pues, simplemente:
como ``identificación''. Escribimos, pues, simplemente:
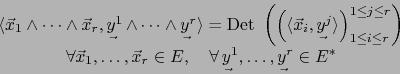
La fórmula (6) se escribe mediante el convenio:
![]()
y dice que, hecha nuestra identificación,
![]() es la base dual de la base
es la base dual de la base
![]() de
de
![]() .
.
![]()
![]() escribimos
de aquí en adelante
escribimos
de aquí en adelante
![]() (sin paréntesis) para cualquiera de
estos dos espacios vectoriales.
(sin paréntesis) para cualquiera de
estos dos espacios vectoriales.
![]() sobre todo elemento descomponible de
sobre todo elemento descomponible de
![]() .
.
![]() de
de
![]() puede escribirse como una suma:
puede escribirse como una suma:
![]()
y todo elemento
![]() puede escribirse como una suma:
puede escribirse como una suma:
![]()
con
![]() descomponibles. Tenemos por bilinealidad del símbolo
descomponibles. Tenemos por bilinealidad del símbolo
![]() :
:
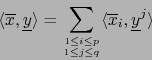
de donde se ve que, en definitiva, la fórmula (8) describe por completo la dualidad entre
![]() y
y
![]() .
.
![]() de
de
![]() y
y
![]() de
de
![]() asociadas a una base
asociadas a una base
![]() de
de ![]() , podemos escribir todo elemento
, podemos escribir todo elemento ![]() de
de
![]() únicamente en la forma:
únicamente en la forma:

y todo elemento ![]() de
de
![]() en la forma:
en la forma:
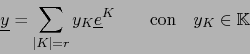
Ya que
![]() es la base dual de la base
es la base dual de la base
![]() , se sigue de ahí, por la observación después del teorema 2.2.1:
, se sigue de ahí, por la observación después del teorema 2.2.1:
![]() -covector sobre cualquier
-covector sobre cualquier ![]() -vector.
-vector.
![]() por una matriz
por una matriz ![]() .
.
![]() . Consideramos unas matrices de elementos en
. Consideramos unas matrices de elementos en ![]() .
.
![]()
Luego ![]() es una matriz de tipo
es una matriz de tipo ![]() .
.
![]() .
.
![]() un espacio vectorial de dimensión
un espacio vectorial de dimensión ![]() sobre
sobre ![]() , provisto de
una base
, provisto de
una base
![]() y
y ![]() su dual provisto de la
base
su dual provisto de la
base
![]() dual del precedente.
dual del precedente.
![]() vectores
vectores
![]() de
de ![]() definidos por:
definidos por:

y los ![]() covectores
covectores
![]() elementos de
elementos de ![]() definidos por:
definidos por:
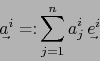
Tenemos
![]() :
:
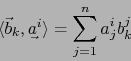
donde el segundo miembro es el elemento de la fila número ![]() y columna número
y columna número ![]() de la matriz producto
de la matriz producto ![]() .
.
![]()
De ahí, por el teorema 2.3.2:
Por otra parte, en virtud del teorema 1.4.18 (sobre las componentes de un
multivector descomponible), vale:
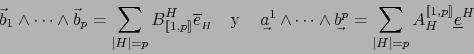
Aquí
![]() y
y
![]() son los menores de
orden
son los menores de
orden ![]() de sendas matrices
de sendas matrices ![]() ,
, ![]() .
.
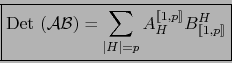
Con las notaciones de nuestra aplicación ![]() es una matriz
es una matriz
![]() . Pero es patentemente de rango
. Pero es patentemente de rango ![]() , luego no es
inversible. Por lo tanto:
, luego no es
inversible. Por lo tanto:
![]()
Subsections
![]()
![]()
![]()
![]()
![]()
Siguiente: Interpretación ``dual'' del producto
Arriba: Aplicaciones multilineales alternadas. Formas
Anterior: El bidual de un
Guillermo M. Luna
2009-06-14