Con las identificaciones
![]() y
y
![]() del teorema 2.2.13 vale:
del teorema 2.2.13 vale:
Con las identificaciones
![]() y
y
![]() del teorema 2.2.13 vale:
del teorema 2.2.13 vale:
Demostración
Sean
![]() elementos arbitrarios. Por definiciones de la aplicación dual de una potencia exterior de
una aplicación lineal y el teorema 2.3.1, obtenemos:
elementos arbitrarios. Por definiciones de la aplicación dual de una potencia exterior de
una aplicación lineal y el teorema 2.3.1, obtenemos:
![]()
Demostración
Sea
![]() . Sean
. Sean
![]() tales que
tales que
![]() . De esta hipótesis se sigue que
. De esta hipótesis se sigue que
![]() ,
pues, de lo contrario, por constituir
,
pues, de lo contrario, por constituir
![]() una base del espacio vectorial
una base del espacio vectorial
![]() de dimensión 1, se seguiría
de dimensión 1, se seguiría
![]() .
.
Usando la definición de determinantes y la relación
![]() que resulta del teorema 2.3.3, obtenemos:
que resulta del teorema 2.3.3, obtenemos:
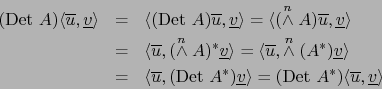
Nota
Sea
![]() una base de
una base de ![]() . Del teorema 2.2.6 se sigue que la matriz de
. Del teorema 2.2.6 se sigue que la matriz de ![]() con respecto a la base
con respecto a la base
![]() de
de ![]() y la matriz de
y la matriz de ![]() con respecto a la base
con respecto a la base
![]() de
de ![]() , dual de la precedente, son
matrices transpuestas una de otra. Por el teorema 1.33 dichas matrices tienen determinantes iguales, de donde se obtiene una nueva demostración del corolario anterior.
, dual de la precedente, son
matrices transpuestas una de otra. Por el teorema 1.33 dichas matrices tienen determinantes iguales, de donde se obtiene una nueva demostración del corolario anterior.
Nuestro corolario es una contrapartida ``intrínseca'' del teorema 1.4.15 que probamos por un mero cálculo sin quitarle el misterio. Por desgracia, con nuestro enfoque no podemos considerar el presente corolario como una demostración del teorema 1.4.15, pues usamos este último como un importante ingrediente de la prueba del teorema 2.3.1 y, por ende, de lo que sigue.