Siguiente: Cambio de ``coeficientes vectoriales'' Arriba: Cambio de base Anterior: Cambio de base en

Cambio de componentes

A. Consideremos un vector $\vec{u} \in E$ que expresamos con respecto a las dos bases como:

$$\fbox{${\displaystyle {\displaystyle \vec{u} = \sum\limits_{i... ...s_{k=1}^n y^k \vec{f}_k ;\quad x^i,\; y^k \in {{\mathbb K}}}}$}$$

Usando las fórmulas (6) obtenemos:

$$x^i= \bigl\langle \vec{u},\mathop{\vtop{\ialign{ ...$$

O sea:

$$\mbox{\fbox{${\displaystyle {\displaystyle x^i = \sum\limits_{k=1}^n s_k^i y^k \;\quad i=1,\ldots,n}}$}}$$ (14)

B. Consideremos un covector que expresamos con respecto a las dos bases duales como:

$$\fbox{${\displaystyle {\displaystyle \mathop{\vtop{\ialign{ ...$$

Usando las fórmulas (1) obtenemos:

$$y_k = \bigl\langle \vec{f}_k,\mathop{\vtop{\ialign{ ...$$

O sea:

$$\mbox{\fbox{${\displaystyle {\displaystyle y_k = \sum\limits_{i=1}^n s_k^i x_i \;,\quad k=1,\ldots,n}}$}}$$ (15)

De nuevo nos encontramos con un ``doble fenómeno de inversión'' al pasar de las fórmulas (14) a las fórmulas (15), a saber:

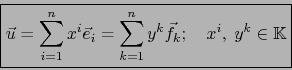
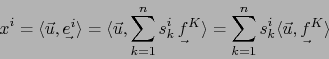
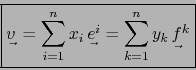
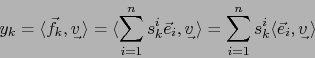
Las fórmulas (14) suministran las ``antiguas'' componentes del vector $\vec u$ en función de las ``nuevas'', mientras que las fórmulas (15) suministran las ``nuevas'' componentes del covector en función de las ``antiguas''.

También la fórmula (14) número $i$ pone en obra la fila núme-romero $i$ de la matriz de transición $\cal S$, mientras la fórmula (15) número $k$ pone en obra la columna número $k$ de dicha matriz.

C. Consideremos un $r$-vector ${\overline u} \in \stackrel{r}{\wedge} E$ que expresamos con respecto a las dos bases asociadas como:

$$\fbox{${\displaystyle {\displaystyle {\overline u}= \sum\limi... ..._{H} = \sum\limits_{\vert K\vert=r} y^{K} {\overline f}_{K}}}$}$$

Usando las fórmulas (13) obtenemos:

$$x^H = \bigl\langle {\overline u},{\underline e}^H\bigr\rangle... ..._K^H \bigl\langle {\overline u},{\underline f}^{K}\bigr\rangle$$

O sea:

$$\mbox{\fbox{${\displaystyle {\displaystyle x^{H}= \sum\limits_{\vert K\vert=r} S_K^H y^{K} \;,\quad \vert H\vert=r}}$}}$$ (16)

Esta fórmula generaliza la fórmula (14).

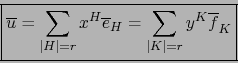
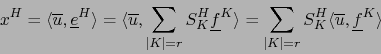
D. Consideremos un $r$-covector ${\underline v} \in \stackrel{r}{\wedge} E^*$ que expresamos con respecto a las dos bases asociadas como:

$$\fbox{${\displaystyle {\displaystyle {\underline v} = \sum\li... ...{H} = \sum\limits_{\vert K\vert=r} y_{K} {\underline f}^{K}}}$}$$

Usando la fórmula (10) conseguimos:

$$y_{K} = \bigl\langle {\overline f}_{K},{\underline v}\bigr\ra... ...K^H \bigl\langle {\overline e}_{H}, {\underline v}\bigr\rangle$$

O sea:

$$\mbox{\fbox{${\displaystyle {\displaystyle y_{K}= \sum\limits_{\vert H\vert=r} S_K^{H} x_{H}}}$}}$$ (17)

fórmula que generaliza (15).

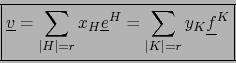
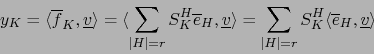
De nuevo hay un ``doble fenómeno de inversión'' al pasar de (16) a (17).

Siguiente: Cambio de ``coeficientes vectoriales'' Arriba: Cambio de base Anterior: Cambio de base en