




Siguiente: Álgebra exterior sobre un
Arriba: Cambio de base
Anterior: Cambio de componentes
Consideremos una forma exterior vectorial de grado 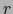 :
:
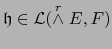 . Según el teorema 2.4.2 expresémosla de dos maneras:
. Según el teorema 2.4.2 expresémosla de dos maneras:
En virtud de la fórmula (10) encontramos:
O sea:
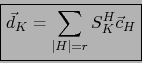 |
(18) |
fórmula análoga a (17).
Observación 1.
Se obtiene fórmulas correctas análogas a las del 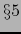 intercambiando la antigua y la nueva base y correspondientemente las antiguas y las nuevas componentes y cambiando la matriz de transición
intercambiando la antigua y la nueva base y correspondientemente las antiguas y las nuevas componentes y cambiando la matriz de transición 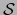 por su inversa:
por su inversa:
Por ejemplo, las fórmulas (14) equivalen a:
Las fórmulas (17) equivalen a:
donde 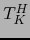 son los menores de orden
son los menores de orden 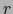 de la matriz
de la matriz 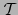 . Las fórmulas (18) equivalen a:
. Las fórmulas (18) equivalen a:
Observación 2.
Para manejar correctamente las fórmulas del 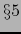 conviene atender a la posición de los índices (o sea, distinguir cuidadosamente entre ``índices superiores'' e ``índices inferiores'') y tener en cuenta las siguientes indicaciones:
conviene atender a la posición de los índices (o sea, distinguir cuidadosamente entre ``índices superiores'' e ``índices inferiores'') y tener en cuenta las siguientes indicaciones:
- Las componentes de multivectores llevan los índices arriba; aquellas de multicovectores llevan los índices abajo.
- Toda sumación se hace sobre un índice mudo que figura en la fórmula una vez arriba y otra abajo.
- El índice libre que figura a la izquierda de cada fórmula figura a la derecha en la misma posición. (Si está abajo a la izquierda estará abajo a la derecha; si está arriba a la izquierda, estará arriba a la derecha.)
- Si trabajamos con la matriz de transición
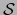 , las fórmulas establecidas suministran:
, las fórmulas establecidas suministran:
- Las antiguas componentes de multivectores en función de las nuevas.
- Las nuevas componentes de multicovectores en función de las antiguas.
Más adelante, al aplicar las fórmulas del 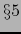 a los ``cambios de mapas'' en variedades diferenciables, veremos cómo en esta aplicación los cálculos se mecanizan todavía más.
a los ``cambios de mapas'' en variedades diferenciables, veremos cómo en esta aplicación los cálculos se mecanizan todavía más.





Siguiente: Álgebra exterior sobre un
Arriba: Cambio de base
Anterior: Cambio de componentes
Guillermo M. Luna
2009-06-14
![]() :
:
![]() . Según el teorema 2.4.2 expresémosla de dos maneras:
. Según el teorema 2.4.2 expresémosla de dos maneras:
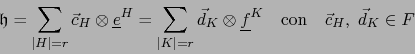
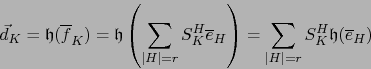
![]() intercambiando la antigua y la nueva base y correspondientemente las antiguas y las nuevas componentes y cambiando la matriz de transición
intercambiando la antigua y la nueva base y correspondientemente las antiguas y las nuevas componentes y cambiando la matriz de transición ![]() por su inversa:
por su inversa:
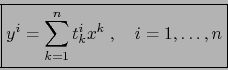
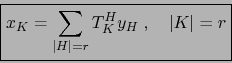
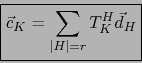
![]() conviene atender a la posición de los índices (o sea, distinguir cuidadosamente entre ``índices superiores'' e ``índices inferiores'') y tener en cuenta las siguientes indicaciones:
conviene atender a la posición de los índices (o sea, distinguir cuidadosamente entre ``índices superiores'' e ``índices inferiores'') y tener en cuenta las siguientes indicaciones: