Siguiente: Espacios vectoriales euclidianos Arriba: Espacios de producto escalar Anterior: El isomorfismo

Fórmulas analíticas

Sea $E$ un espacio de producto escalar provisto de una base $(\vec{e}_1,\ldots,\vec{e}_n)$. Como de costumbre, designamos por la base de $E^*$ dual de ésta. Notamos por:

$$\fbox{${\displaystyle \left[ G \right] = ( g_{ik} )_{1 \le i,k \le n}}$}$$

la matriz del isomorfismo $G \colon E \to E^*$ con respecto a dichas bases. Rigen, pues, las fórmulas:

$$\mbox{\fbox{${\displaystyle {\displaystyle G \vec{e}_k = \sum... ...echa$\cr\noalign{\kern-5pt}}}}\limits \quad k=1,\ldots,n} }$}}$$ (18)

$\lbrack G \rbrack$ es una matriz de tipo $n\times n$. Puesto que $G$ es un isomorfismo, dicha matriz es inversible. Puesto que $G$ es una aplicación lineal simétrica de $E$ en $E^*$, dicha matriz es simétrica, es decir, vale:

$$\fbox{${\displaystyle g_{ki} = g_{ik} \quad \forall i,\,k \in \lbrack\!\lbrack 1,n \rbrack\!\rbrack }$}$$

La matriz del isomorfismo inverso $G^{-1}\colon E^* \to E$ es $\lbrack G \rbrack^{-1}$, la matriz inversa de la matriz $\lbrack G \rbrack$. Introducimos la notación:

$$\fbox{${\displaystyle \lbrack G \rbrack^{-1} = (g^{ik})^{1 \le i,k \le n}}$}$$

Rigen las fórmulas:

$$\mbox{\fbox{${\displaystyle {\displaystyle G^{-1} \mathop{\vt... ...limits = \sum_{k=1}^n g^{ki} \vec{e}_k \quad i=1,\ldots,n}}$}}$$ (19)

Puesto que $G^{-1}$ es una aplicación lineal simétrica de $E^*$ en $E=E^{**}$ la matriz $\lbrack G \rbrack^{-1}$ es también una matriz simétrica, o sea:

$$\fbox{${\displaystyle g^{ki}=g^{ik}}$}$$

La posición de los índices (arriba o abajo) es evidentemente aquí esencial.

A. Expresiones de productos escalares. Por definición del isomorfismo $G$ tenemos:

$$\forall i,\,j \in \lbrack\!\lbrack 1,n \rbrack\!\rbrack \ \ (... ...rt\vec{e}_k) = \bigl\langle \vec{e}_i, G \vec{e}_k\bigr\rangle$$

o sea, por la fórmula (18):

$$\mbox{\fbox{${\displaystyle (\vec{e}_i \vert \vec{e}_k ) = g_... ...uad \forall i,k \in \lbrack\!\lbrack 1,n \rbrack\!\rbrack }$}}$$ (20)

Asimismo, usando (19):

$$(\mathop{\vtop{\ialign{ ...$$

o sea:

$$\mbox{\fbox{${\displaystyle (\mathop{\vtop{\ialign{ ...$$ (21)

Las fórmulas (20) y (21) pueden servir de definiciones alternativas de los elementos $g_{ik}$ y $g^{ik}$ de sendas matrices $\lbrack G \rbrack$ y $\lbrack G \rbrack^{-1}$ y son preferidas como tales por libros elementales. Se logra, sin embargo, una mejor perspectiva, si se interpreta en lo posible toda matriz como matriz de una aplicación lineal con respecto a bases convenientes. Sean:

$$\vec{x}= \sum_{i=1}^n x^i \vec{e}_i,\quad \vec{y}= \sum_{k=1}^n y^k \vec{e}_k$$

vectores arbitrarios de $E$. Por la bilinealidad del producto escalar obtenemos:

$$(\vec{x}\vert\vec{y}) = \sum\limits_{1\le i \le n \atop 1 \le k \le n} x^i y^k (\vec{e}_i\vert\vec{e}_k)$$

o sea, haciendo uso de (20):

$$\mbox{\fbox{${\displaystyle {\displaystyle (\vec{x}\vert \vec... ...\limits_{1 \le i\le n \atop 1\le k \le n} g_{ik} x^i y^k }}$}}$$ (22)

Sean ahora:

$$\mathop{\vtop{\ialign{ ...$$

covectores arbitrarios, elementos de $E^*$. Se tiene:

$$(\mathop{\vtop{\ialign{ ...$$

o sea, por (21):

$$\mbox{\fbox{${\displaystyle {\displaystyle (\mathop{\vtop{\ia... ...m\limits_{1 \le i \le n \atop 1\le k\le n} g^{ik} x_i y_k}}$}}$$ (23)

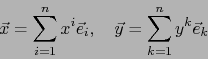
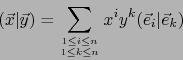
B. Componentes contravariantes y componentes covariantes de un vector. Sea $\vec{x} = \sum_{i=1}^n x^i \vec{e}_i$ un vector arbitrario. Las componentes (usuales) $x^i$ de $\vec x$ con respecto a la base $(\vec{e}_1,\ldots,\vec{e}_n)$ las llamaremos COMPONENTES CONTRAVARIANTES DEL VECTOR $\vec{x}$ con respecto a dicha base. Escribimos:

$$\mbox{\fbox{${\displaystyle {\displaystyle G \vec{x} = \sum\l... ...nterlineskip} $\flecha$\cr\noalign{\kern-5pt}}}}\limits }}$}}$$ (24)

Las componentes $x_i$ del covector $G\vec{x}$ con respecto a la base dual se llaman las COMPONENTES COVARIANTES DEL VECTOR $\vec x$ con respecto a la base $(\vec{e}_1,\ldots,\vec{e}_n)$.

Usando la fórmula (24) obtenemos:

$$x_i = \bigl\langle \vec{e}_i, G\vec{x} \bigr\rangle$$

o sea:

$$\mbox{\fbox{${\displaystyle x_i = (\vec{e}_i\vert \vec{x}) }$}}$$ (25)

La fórmula (25) expresa las componentes covariantes $x_i$ del vector $\vec x$ sin referencia explícita al isomorfismo $G$. Puede servir de definición alternativa de las componentes covariantes.

Cálculo de las componentes covariantes de $\vec{x}$ en función de las componentes contravariantes. Sea $\vec{x} = \sum_{k=1}^n x^k \vec{e}_k \; \in E$. Por la fórmula (25):

$$x_i=\left( \vec{e}_i \biggm\vert \sum_{k=1}^n x^k \vec{e}_k \right) = \sum_{k=1}^n x^k (\vec{e}_i\vert \vec{e}_k)$$

de donde por (20):

$$\mbox{\fbox{${\displaystyle {\displaystyle x_i = \sum_{k=1}^n g_{ik} x^k }}$}}$$ (26)

Esta fórmula (26) se llama la FÓRMULA DEL DESCENSO DEL ´iNDICE.

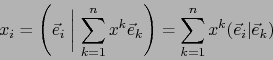
Cálculo de las componentes contravariantes de $\vec x$ en función de las componentes covariantes. Usando la fórmula (19) obtenemos:

$$x^i = \bigl\langle \vec{x},\mathop{\vtop{\ialign{ ...$$

o sea, por (25):

$$\mbox{\fbox{${\displaystyle {\displaystyle x^i = \sum_{k=1}^n g^{ki} x_k }}$}}$$ (27)

Ésta es la FÓRMULA DEL ASCENSO DEL ´iNDICE.

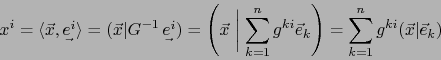
Usando las fórmulas (26) y (27) podemos transformar la expresión (22) del producto escalar. Usando (26) obtenemos:

$$(\vec{x}\vert \vec{y}) = \sum_{1 \le i \le n \atop 1\le j \le... ...eft( \sum_{i=1}^n g_{ij} x^i \right) y^j = \sum_{j=1}^n x_j y^j$$

De ahí, por la simetría del producto escalar:

$$(\vec{x}\vert\vec{y}) = (\vec{y}\vert\vec{x}) = \sum_{j=1}^n y_j x^j = \sum_{j=1}^n x^j y_j$$

y, finalmente, usando esta última fórmula y (27):

$$(\vec{x}\vert\vec{y}) = \sum_{j=1}^n \left( \sum_{i=1}^n g^{i... ... y_j = \sum_{1 \le i \le n \atop 1 \le j \le n } g^{ij} x_i y_j$$

En resumen:

$$\mbox{\fbox{${\displaystyle (\vec{x}\vert\vec{y}) = \sum\limi... ...sum\limits_{1\le i\le n \atop 1\le j \le n} g^{ij} x_i y_j}$}}$$ (28)

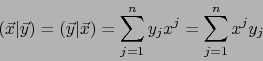
C. Componentes covariantes y contravariantes de un covector. Sea

$$\mathop{\vtop{\ialign{ ...$$ (29)

un covector, elemento de $E^*$. Las componentes (usuales) $x_i$ de con respecto a la base se llaman las COMPONENTES COVARIANTES DEL COVECTOR . Sea:

$$G^{-1} \mathop{\vtop{\ialign{ ...$$ (30)

Las componentes $x^i$ del vector con respecto a la base $(\vec{e}_1,\ldots,\vec{e}_n)$ se llaman las COMPONENTES CONTRAVARIANTES DEL COVECTOR . Notamos que, por la fórmula (30):

$$x^i = \bigl\langle G^{-1} \mathop{\vtop{\ialign{ ...$$

o sea:

$$\fbox{${\displaystyle x^i = (\mathop{\vtop{\ialign{ ...$$

fórmula análoga a (25) que permite definir las componentes contravariantes del covector sin referencia explícita al isomorfismo $G$.

Al introducir el vector transformamos las fórmulas (30) y (29) respectivamente en:

$$\vec{x}= \sum\limits_{i=1}^n x^i \vec{e}_i \quad \mbox{y} \qu... ...pt\nointerlineskip} $\flecha$\cr\noalign{\kern-5pt}}}}\limits$$

De ahí vemos que las componentes covariantes (resp. contravariantes) del covector son las mismas que las componentes covariantes (resp. contravariantes) del vector $\vec x$.

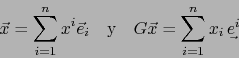
Por lo tanto, las fórmulas (26) y (27) del descenso y ascenso del índice siguen válidas sin cambio para las componentes de misma denominación de un covector.

Finalmente, sean dos covectores y sean los vectores correspondientes. Puesto que $G$ es una isometría de $E$ sobre $E^*$ tenemos , o sea, por (28):

$$\fbox{${\displaystyle {\displaystyle (\mathop{\vtop{\ialign{ ...$$

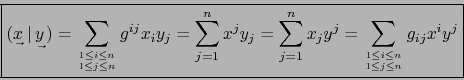
Nota 1. (Sobre la terminología)

La terminología de componentes ``contravariantes'' y ``covariantes'', como la usamos, llegó a ser tradicional. Los físicos van al punto de llamar ``vectores contravariantes'' a los elementos de $E$ y ``vectores covariantes'' a los elementos de $E^*$. Por desgracia, según la óptica actual de la matemática, esa terminología (cuya justificación es bastante obscura) es totalmente impropia y hasta existen buenas razones para invertirla.

En efecto, un diagrama:

$$E \smash{ \mathop{\longrightarrow}\limits^{A}} F \smash{ \mathop{\longrightarrow}\limits^{B}} G$$

de espacios vectoriales $E, \, F, \, G$ y aplicaciones lineales $A,\, B$ da lugar, como sabemos, al diagrama:

$$E^* \smash{ \mathop{\longleftarrow}\limits^{A^*}} F^* \smash{ \mathop{\longleftarrow}\limits^{B^*}} G^*$$

con flechas invertidas y vale la fórmula:

$$(B\circ A)^* = A^* \circ B^*$$

con una inversión del orden de los factores.

En vista de ello, sería natural llamar a los elementos de $E$ entes ``covariantes'' y a aquellos de $E^*$ entes ``contravariantes'' en flagrante oposición con la costumbre. Dicha costumbre está, sin embargo, tan arraigada en la literatura matemática, y más todavía, física, que ni el presente autor ni probablemente ningún otro se atrevería a invertirla.

Una salida a tal dificultad podría darse en algún futuro, abandonando por completo en este contexto las palabras ``componentes contravariantes'' y ``componentes covariantes'' y substituyéndolas por otras, posiblemente más sugestivas. Yo propondría ``componentes vectoriales'' y ``componentes duales''.

En cuanto a la terminología de ``vectores contravariantes'' y ``vectores covariantes'', es afortunadamente inútil y la solución del problema es simplemente no usarla.

Nota 2.

Arriesgando un lenguaje sumamente informal, vamos a tratar de justificar ``intuitivamente'' el uso de dobles componentes.

El isomorfismo $G$ ``canónico por fuerza bruta'' de $E$ sobre $E^*$, en la teoría de espacios de producto escalar, permitiría identificar $E^*$ con $E$. Informalmente, podemos pensar en dicha identificación y hablar, como se hace ya de manera común, de la ``autodualidad'' de un espacio de producto escalar (oficialmente no realizaremos esta identificación, pues ello no contribuiría a la claridad de la exposición).

En la óptica de la considerada identificación, un vector $\vec{x} \in E$ y un covector tales que , equivalentemente pueden considerarse como una misma persona con dos nacionalidades. Como $\vec{x}$, dicha persona es un ciudadano de $E$, mas como , es un ciudadano de $E^*$. Como ciudadano de $E$ posee las componentes $x^i$ con respecto a una base $(\vec{e}_1,\ldots,\vec{e}_n)$ de $E$. Como ciudadano de $E^*$ posee las componentes $x_i$ con respecto a la base dual de la precedente.

Algunos libros, que sus autores destinan a ingenieros o físicos experimentales, hacen la identificación $E \approx E^*$ implícitamente, pero radicalmente, ocultando por completo $E^*$ y hablando solamente del espacio de producto escalar $E$. Esto les conduce a asociar con toda base $(\vec{e}_1,\ldots,\vec{e}_n)$ de $E$ a otra base del mismo $E$, la cual, en nuestra notación no es otra que y que llaman ``base recíproca'' de la anterior. La caracterizan geométricamente y prueban que la recíproca de la última es la base inicial. Mucha perspectiva no se gana con tal enfoque, aunque sea conforme al desarrollo histórico de la teoría. En efecto, el concepto de dualidad surgió relativamente tarde en álgebra lineal.

Siguiente: Espacios vectoriales euclidianos Arriba: Espacios de producto escalar Anterior: El isomorfismo