




Siguiente: Matriz de
Arriba: Álgebra exterior sobre un
Anterior: Álgebra exterior sobre un
Sea  un espacio vectorial de dimensión finita y sea
un espacio vectorial de dimensión finita y sea 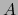 una aplicación lineal de
una aplicación lineal de  en su espacio dual
en su espacio dual 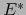 . La aplicación
. La aplicación 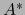 , dual de la aplicación lineal
, dual de la aplicación lineal 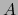 es una aplicación lineal del bidual
es una aplicación lineal del bidual 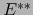 en
en 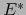 . Al identificar dicho bidual según el
convenio después del teorema 2.2.10 con
. Al identificar dicho bidual según el
convenio después del teorema 2.2.10 con  , tendremos simplemente:
, tendremos simplemente:
Precisemos la definición de 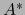 en presencia de nuestra identificación. Al designar provisionalmente por
en presencia de nuestra identificación. Al designar provisionalmente por 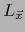 el elemento del bidual
el elemento del bidual 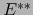 que se identifica con el vector
que se identifica con el vector 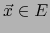 , tenemos por definición de la aplicación dual
, tenemos por definición de la aplicación dual
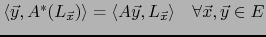 o sea,
con la identificación
o sea,
con la identificación 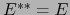 :
:
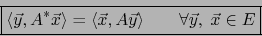 |
(1) |
Note que al pasar del primero al segundo miembro de (1), se intercambian los vectores
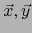 y se cambia
y se cambia 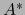 por
por 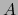 .
.
A continuación no se tratará de aplicaciones lineales antisimétricas.
Esto es una consecuencia inmediata de la definición y de la fórmula (1) de arriba.
Corolario 1.1
Sea
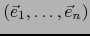 una base de
una base de  . Una aplicación lineal
. Una aplicación lineal
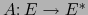 es una aplicación lineal simétrica si y sólo si:
es una aplicación lineal simétrica si y sólo si:
Subsections





Siguiente: Matriz de
Arriba: Álgebra exterior sobre un
Anterior: Álgebra exterior sobre un
Guillermo M. Luna
2009-06-14
![]() un espacio vectorial de dimensión finita y sea
un espacio vectorial de dimensión finita y sea ![]() una aplicación lineal de
una aplicación lineal de ![]() en su espacio dual
en su espacio dual ![]() . La aplicación
. La aplicación ![]() , dual de la aplicación lineal
, dual de la aplicación lineal ![]() es una aplicación lineal del bidual
es una aplicación lineal del bidual ![]() en
en ![]() . Al identificar dicho bidual según el
convenio después del teorema 2.2.10 con
. Al identificar dicho bidual según el
convenio después del teorema 2.2.10 con ![]() , tendremos simplemente:
, tendremos simplemente: