Sea E un espacio de producto escalar. Para un vector fijo ![]() consideremos la aplicación
consideremos la aplicación
![]() de
de ![]() en
en ![]() . Por el axioma i) de espacio de producto escalar, esta aplicación es lineal, o sea, es una forma lineal sobre
. Por el axioma i) de espacio de producto escalar, esta aplicación es lineal, o sea, es una forma lineal sobre ![]() , elemento de
, elemento de ![]() . La llamaremos
. La llamaremos ![]() . Así pues:
. Así pues:
Demostración
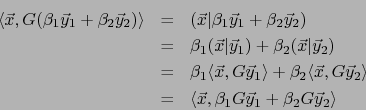
Así queda probado que ![]() es una aplicación lineal inyectiva de
es una aplicación lineal inyectiva de ![]() en
en ![]() .
Pero siendo
.
Pero siendo
![]() , se sigue de ahí sin más que
, se sigue de ahí sin más que ![]() es un isomorfismo lineal de
es un isomorfismo lineal de ![]() sobre
sobre ![]() .
.
![]()
He aquí el teorema recíproco:
Demostración
En lenguaje menos formal: dar un isomorfismo simétrico ![]() de
de ![]() sobre
sobre ![]() es lo mismo que dar un producto escalar
es lo mismo que dar un producto escalar
![]() . Las dos cosas se relacionan por la fórmula:
. Las dos cosas se relacionan por la fórmula:
Nota
Si ![]() es un espacio vectorial de dimensión finita, vale
es un espacio vectorial de dimensión finita, vale
![]() , luego
, luego ![]() y
y ![]() son espacios vectoriales isomorfos. Pero, sin más estructura sobre
son espacios vectoriales isomorfos. Pero, sin más estructura sobre ![]() , no podemos dar un isomorfismo ``canónico'' (o ``natural'') de
, no podemos dar un isomorfismo ``canónico'' (o ``natural'') de ![]() sobre
sobre ![]() , es decir, uno independiente de elecciones arbitrarias, aquí de la elección de una base. La situación es distinta si
, es decir, uno independiente de elecciones arbitrarias, aquí de la elección de una base. La situación es distinta si ![]() es un espacio de producto escalar, pues en este caso disponemos del isomorfismo canónico
es un espacio de producto escalar, pues en este caso disponemos del isomorfismo canónico ![]() y éste determina la estructura de
y éste determina la estructura de ![]() como espacio de producto escalar. Estamos en presencia, por decirlo
así, de un isomorfismo canónico de
como espacio de producto escalar. Estamos en presencia, por decirlo
así, de un isomorfismo canónico de ![]() sobre
sobre ![]() ``impuesto por fuerza bruta''.
``impuesto por fuerza bruta''.
Este trozo de charla arroja, quizá, algo de luz sobre el elusivo concepto de ``canónico''. Algo es ``canónico'' siempre relativamente a una estructura considerada. Cuando ésta se enriquezca, aparecen nuevos elementos ``canónicos''.
Demostración
Usando el teorema 2.2.5 y la relación ![]() obtenemos:
obtenemos:
Podemos también decir que el producto escalar sobre ![]() se obtiene transportando sobre
se obtiene transportando sobre ![]() mediante el isomorfismo
mediante el isomorfismo ![]() el producto escalar sobre
el producto escalar sobre ![]() .
.
Los tres axiomas del producto escalar entrañan las siguientes propiedades de ortogonalidad:

Si ![]() es una parte de
es una parte de ![]() y
y ![]() , escribimos abreviadamente:
, escribimos abreviadamente:
![]() en vez de
en vez de
![]() .
.
Notamos que las propiedades i) y iii) de la ortogonalidad implican respectivamente:
Demostración
Rige la cadena de equivalencias:
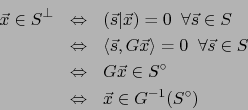
Esto se ve inmediatamente por definición. También por los teoremas 2.2.8 y 3.1.6:
Demostración
Por el teorema 2.2.8 tenemos:
Nota
El teorema 3.1.8 permite, al estudiar subespacios ortogonales a subconjuntos de ![]() , limitarse al caso de ser dichos subconjuntos subespacios de
, limitarse al caso de ser dichos subconjuntos subespacios de ![]() .
.
Demostración
Por el teorema 2.2.9 vale:
Demostración
La definición implica inmediatamente:
Como consecuencia inmediata del teorema 3.1.10, obtenemos:
Advertencia
Si ![]() es un subespacio de
es un subespacio de ![]() , no se tiene en general:
, no se tiene en general:
Un vector no nulo de ![]() que cumple con (17) se llama un VECTOR ISÓTROPO de
que cumple con (17) se llama un VECTOR ISÓTROPO de ![]() .
.