Para todo par de elementos:
![]() de
de
![]() definamos:
definamos:
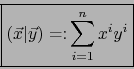
El producto escalar canónico se usa con más frecuencia en el caso real
![]() . Define sobre
. Define sobre
![]() una estructura de espacio vectorial euclidiano llamada ESTRUCTURA CANÓNICA DE ESPACIO VECTORIAL EUCLIDIANO sobre
una estructura de espacio vectorial euclidiano llamada ESTRUCTURA CANÓNICA DE ESPACIO VECTORIAL EUCLIDIANO sobre
![]() .
.
Demostración
En virtud del teorema 3.1.13, basta demostrar la primera afirmación. Sea
![]() una base O.N. de
una base O.N. de ![]() . Por la condición 2, después de las definiciones 3.1.7, tenemos:
. Por la condición 2, después de las definiciones 3.1.7, tenemos: