Siguiente: El operador de Hodge Arriba: Álgebra exterior sobre un Anterior: Producto escalar canónico en

Producto escalar inducido en $\stackrel{r}{\wedge}E$ y en $\stackrel{r}{\wedge} E^*$

Teorema 2.1 (y definiciones)   Sean $E$ un espacio de producto escalar y $G$ el correspondiente isomorfismo simétrico de $E$ sobre $E^*$. Sea $r\in \lbrack\!\lbrack 0,n \rbrack\!\rbrack$. $\stackrel{r}{\wedge} G$ es un isomorfismo simétrico del espacio vectorial $\stackrel{r}{\wedge}E$ sobre su dual $\stackrel{r}{\wedge} E^*$. Define sobre $\stackrel{r}{\wedge}E$ la estructura de espacio de producto escalar dicha ESTRUCTURA DE ESPACIO DE PRODUCTO ESCALAR SOBRE #MATH3032# INDUCIDA por la de $E$.

Si $(\vec{x}_1,\ldots,\vec{x}_r),\,(\vec{y}_1,\ldots,\vec{y}_r)$ son sendos $r$-uplos de vectores de $E$, vale para dichas estructuras:

$$\mbox{\fbox{${\displaystyle (\vec{x}_1 \wedge \cdots \wedge \... ...t(\vec{x}_i\vert\vec{y}_j \right)_{1 \le i,j\le r} \right)}$}}$$ (1)

En particular:

$$\fbox{${\displaystyle (\vec{x}_1 \wedge \cdots \wedge \vec{x}... ...eft(\vec{x}_i\vert\vec{x}_j \right)_{1 \le i,j\le r} \right)}$}$$

El determinante a la derecha de la última fórmula se llama DETERMINANTE DE GRAM o GRAMIANO del $r$-uplo $(\vec{x}_1,\ldots,\vec{x}_r)$.

Demostración
Siendo $G$ un isomorfismo lineal de $E$ sobre $E^*$, por el corolario del teorema 1.4.7 $\stackrel{r}{\wedge} G$ es un isomorfismo del espacio vectorial $\stackrel{r}{\wedge}E$ sobre su dual $\stackrel{r}{\wedge} E^*$. También por el teorema 2.3.3:

$$(\stackrel{r}{\wedge} G)^* = \stackrel{r}{\wedge}( G^*)$$

y, puesto que $G^* = G$, esto reza:

$$(\stackrel{r}{\wedge} G)^* = \stackrel{r}{\wedge} G$$

Así pues, $\stackrel{r}{\wedge} G$ es un isomorfismo simétrico del espacio vectorial $\stackrel{r}{\wedge}E$ sobre su dual $\stackrel{r}{\wedge} E^*$.

En virtud del teorema 3.1.4, induce sobre el espacio vectorial $\stackrel{r}{\wedge}E$ una estructura de espacio de producto escalar, siendo:

$$({\overline u}\vert {\overline v}) =\bigl\langle {\overline ... ... \, {\overline u},\, {\overline v} \in \stackrel{r}{\wedge} E$$ (2)

Sean $(\vec{x}_1,\ldots,\vec{x}_r),\,(\vec{y}_1,\ldots,\vec{y}_r)$ dos $r$-uplos de vectores de $E$. Al tomar en (2): ${\overline u}=\colon \vec{x}_1 \wedge \cdots \wedge \vec{x}_r$ y ${\overline v}=\colon \vec{y}_1 \wedge \cdots \wedge \vec{y}_r$ obtenemos por el teorema 2.3.1

$$\begin{eqnarray*} (\vec{x}_1 \wedge \cdots \wedge \vec{x}_r \vert \vec{y}_1 \wed... ...t( ( \vec{x}_i\vert \vec{y}_j) \right)_{1 \le i,j \le n} \right) \end{eqnarray*}$$

$\quad\Box$

Observación 1.

Puesto que $\stackrel{0}{\wedge} G$ es la identidad sobre $\stackrel{0}{\wedge} E = {\mathbb{K}}$, el producto escalar de dos elementos $\alpha,\, \beta \in {\mathbb{K}}$ es $\alpha \beta$, el producto usual en ${\mathbb{K}}$.

Observación 2.

Sean $(\vec{e}_1,\ldots,\vec{e}_n)$ y una base de $E$ y la base de $E^*$ dual de ésta. Sean $({\overline e}_H)_{\vert H\vert=r}$ y $({\underline e}^H)^{\vert H\vert=r}$ las bases de sendos espacios $\stackrel{r}{\wedge} E, \, \stackrel{r}{\wedge} E^*$ asociadas a las anteriores. Por el teorema 1.4.19 tenemos:

$$(\stackrel{r}{\wedge} G) {\overline e}_H = \sum_{\vert K\vert=r} G_{K,H} {\underline e}^K \,, \; \vert H\vert=r$$

donde $G_{K,H}$ son los menores de orden $r$ de la matriz $[G]=(g_{ik})_{1 \le i,k \le n}$. Vale pues:

$$\fbox{${\displaystyle ({\overline e}_H\vert {\overline e}_K) = G_{H,K}}$}$$

De ahí el producto escalar de dos $r$-vectores arbitrarios ${\overline u} = \sum_{\vert H\vert=r} x^H {\overline e}_H$, ${\overline v}= \sum_{\vert K\vert=r} y^K {\overline e}_K$ se expresa por la fórmula:

$$\mbox{\fbox{${\displaystyle {\displaystyle ({\overline u}\ver... ...ts_{\vert H\vert=r \atop \vert K\vert=r} G_{H,K} x^H y^K }}$}}$$ (3)

Por contraste, la fórmula (1) del teorema 3.2.1 suministra explícita y solamente el producto escalar de $r$-vectores descomponibles, aunque sobre la fórmula (3) tiene la ventaja de ser intrínseca.

Teorema 2.2   Sea $E$ un espacio de producto escalar. Si $(\vec{e}_1,\ldots,\vec{e}_n)$ es una base O.N. de $E$, también lo es la base $({\overline e}_H)_{\vert H\vert=r}$ de $\stackrel{r}{\wedge}E$. Si $E$ es un espacio vectorial euclidiano, también lo es $\stackrel{r}{\wedge}E$.

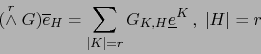
Demostración
En virtud del teorema 3.1.13 basta probar la primera afirmación. Sea $(\vec{e}_1,\ldots,\vec{e}_n)$ una base O.N. de $E$. Sean $H,\,K$ partes de $\lbrack\!\lbrack 1,n \rbrack\!\rbrack$ de cardinalidad $r$:

$$H = \{ i_1,\ldots,i_r \} \,,\, i_1< \cdots < i_r \; , \; K = \{ j_1,\ldots,j_r \} \,,\, j_1< \cdots < j_r$$

Por la fórmula (1) del teorema 3.2.1:

$$\begin{eqnarray*} ({\overline e}_H \vert {\overline e}_K)&=& (\vec{e}_{i_1} \wed... ...Det } ( \delta_{i_\alpha , i_\beta})_{1 \le \alpha, \beta \le r} \end{eqnarray*}$$

o sea, por el lema 2.1:

$$({\overline e}_H\vert {\overline e}_K)= \delta_{H,K} \, .$$

Así pues, la base $({\overline e}_H)_{\vert H\vert=r}$ es una base O.N. de $\stackrel{r}{\wedge}E$. $\quad\Box$

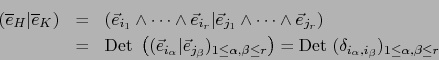
Otra demostración.

Usamos la condición 2 después de las definiciones 3.1.7. Por ella vale:

$$G \vec{e}_i = \mathop{\vtop{\ialign{ ...$$

De ahí , si $H=\{i_1,\ldots,i_r\} \,,\; i_1< \cdots <i_r$:

$$\begin{eqnarray*} \stackrel{r}{\wedge} G({\overline e}_H) &=& \stackrel{r}{\wedg... ...p} $\flecha$\cr\noalign{\kern-5pt}}}}\limits = {\underline e}^H \end{eqnarray*}$$

De nuevo, por dicha condición 2, esto prueba que $({\overline e}_H)_{\vert H\vert=r}$ es una base O.N. de $\stackrel{r}{\wedge}E$.

Teorema 2.3   Sean $E$ un espacio de producto escalar y $G$ el correspondiente isomorfismo simétrico de $E$ sobre $E^*$.

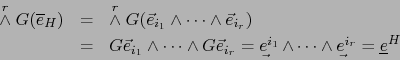
La aplicación $\stackrel{r}{\wedge} ( G^{-1}) =( \stackrel{r}{\wedge} G )^{-1}$ (la notaremos simplemente $\stackrel{r}{\wedge} G^{-1}$) es un isomorfismo simétrico del espacio vectorial $\stackrel{r}{\wedge} E^*$ sobre su dual $\stackrel{r}{\wedge}E$. Define sobre $\stackrel{r}{\wedge} E^*$ una estructura de espacio de producto escalar dicha ESTRUCTURA DE ESPACIO DE PRODUCTO ESCALAR INDUCIDA por la de $E$. $\stackrel{r}{\wedge} G$ es una isometría de $\stackrel{r}{\wedge}E$ sobre $\stackrel{r}{\wedge} E^*$ y $\stackrel{r}{\wedge} G^{-1}$ es la isometría inversa de $\stackrel{r}{\wedge} E^*$ sobre $\stackrel{r}{\wedge}E$.

Si son dos $r$-uplos de covectores, elementos de $E^*$ vale:

$$\fbox{${\displaystyle (\mathop{\vtop{\ialign{ ...$$

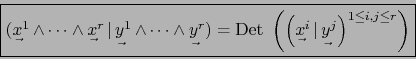
Demostración
Por el teorema 3.2.1 la aplicación $\stackrel{r}{\wedge} G$ es un isomorfismo simétrico del espacio vectorial $\stackrel{r}{\wedge}E$ sobre su dual. Por el corolario del teorema 1.4.7 la aplicación inversa de ésta es $(\stackrel{r}{\wedge} G)^{-1} = \stackrel{r}{\wedge}( G^{-1})$. Como hemos dicho, la notaremos simplemente $\stackrel{r}{\wedge} G^{-1}$.

Por el teorema 3.1.5, dicha inversa $\stackrel{r}{\wedge} G^{-1}$ es un isomorfismo simétrico del espacio vectorial $\stackrel{r}{\wedge} E^*$ sobre su dual $\stackrel{r}{\wedge}E$. Define sobre $\stackrel{r}{\wedge} E^*$ una estructura de espacio de producto escalar.

Por la fórmula (2) en la demostración del teorema 3.1.5 vale:

$$\fbox{${\displaystyle ({\underline u}\vert {\underline v}) = ... ...underline u},\, {\underline v} \in \stackrel{r}{\wedge} E^* }$}$$

Por el mismo teorema 3.1.5, $\stackrel{r}{\wedge} G$ es una isometría de $\stackrel{r}{\wedge} E^*$ y $\stackrel{r}{\wedge} G^{-1}$ es la isometría inversa. Se sigue de ahí y del teorema 3.2.1 que si , son $r$-uplos de covectores, elementos de $\stackrel{r}{\wedge} E^*$ vale:

$$\begin{eqnarray*} &\ & (\mathop{\vtop{\ialign{ ...$$

$\quad\Box$

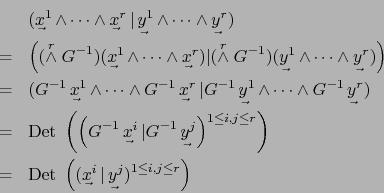
Observación
Sean $(\vec{e}_1,\ldots \vec{e}_n)$ una base de $E$ y las bases asociadas de sendos espacios vectoriales $E^*,\, \stackrel{r}{\wedge} E ,\, \stackrel{r}{\wedge} E^*$. Por el teorema 1.4.19 las relaciones:

$$\mathop{\vtop{\ialign{ ...$$

implican:

$$\fbox{${\displaystyle {\displaystyle {\underline e}^H = \sum_... ...rt=r} G^{K,H} {\overline e}_K ,\hspace{3em} \vert H\vert=r }}$}$$

donde $G^{K,H}$ son los menores de orden $r$ de la matriz $[G]^{-1} = (g^{ij})^{1 \le i,j \le n}$, luego:

$$\fbox{${\displaystyle ({\underline e}^H\vert {\underline e}^K) = G^{H,K}}$}$$

Si ${\underline u}= \sum_{\vert H\vert=r} x_H {\underline e}^H \,, \; {\underline v} = \sum_{\vert K\vert=r} y_K {\underline e}^K$, vale:

$$\fbox{${\displaystyle {\displaystyle ({\underline u}\vert{\un... ...ne v}) = \sum_{\vert K\vert=\vert H\vert=r} G^{H,K} x_H y_K}}$}$$

Teorema 2.4   Sea $E$ un espacio de producto escalar. Si $(\vec{e}_1,\ldots,\vec{e}_n)$ es una base O.N. de $E$, $({\underline e}^H)^{\vert H\vert=r}$ es una base O.N. de $\stackrel{r}{\wedge} E^*$. Si $E$ es un espacio vectorial euclidiano, también $\stackrel{r}{\wedge} E^*$ es un espacio vectorial euclidiano.

Demostración
En virtud del teorema 3.1.13, basta probar la primera afirmación.

Sea $(\vec{e}_1,\ldots,\vec{e}_n)$ una base O.N. de $E$. Por el teorema 3.2.2, $({\overline e}_H)_{\vert H\vert=r}$ es una base O.N. de $\stackrel{r}{\wedge}E$. Pero por el teorema 2.3.1 la base $({\underline e}^H)^{\vert H\vert=r}$ de $\stackrel{r}{\wedge} E^*$ es la base dual de la base $({\overline e}_H)_{\vert H\vert=r}$ de $\stackrel{r}{\wedge}E$. Luego por el teorema 3.1.16, la base $({\underline e}^H)^{\vert H\vert=r}$ es una base O.N. de $\stackrel{r}{\wedge} E^*$. $\quad\Box$

Teorema 2.5   Sea $E$ un espacio de producto escalar. Si $\vec{x}_1,\ldots,\vec{x}_{p+q} \in E$, ${\overline y} \in \stackrel{p}{\wedge} E$, ${\overline z} \in \stackrel{q}{\wedge} E$ vale (con las notaciones del teorema 2.3.2):

$$\fbox{${\displaystyle {\displaystyle (\vec{x}_1 \wedge \cdots... ...verline y}) ( {\overline x}_{H^\prime} \vert{\overline z}) }}$}$$

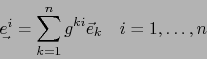
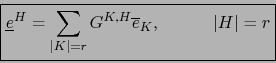
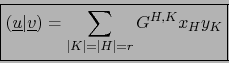
Demostración
Por la observación después de la definición 3.1.4 y el teorema 2.3.2 tenemos:

$$\begin{eqnarray*} (\vec{x}_1 \wedge \cdots \wedge \vec{x}_{p+q} \vert {\overline... ...ert {\overline y}) ({\overline x}_{H^\prime} \vert{\overline z}) \end{eqnarray*}$$

Teorema 2.6   Sea $E$ un espacio de producto escalar. Para $p+q$ covectores y dos formas ${\underline y} \in \stackrel{p}{\wedge} E^*$, ${\underline z} \in \stackrel{q}{\wedge} E$ vale:

$$\fbox{${\displaystyle {\displaystyle (\mathop{\vtop{\ialign{ ...$$

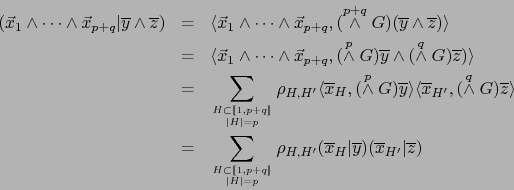
Demostración
Puesto que $\stackrel{p+q}{\wedge} G^{-1}$ es una isometría de $\stackrel{p+q}{\wedge} E^*$ sobre $\stackrel{p+q}{\wedge} E$ tenemos:

$$=$$

$$=$$ (4)

Por otra parte, aplicando el teorema 3.2.5 obtenemos:

$$\begin{array}[b]{ll} \ &\Bigl( G^{-1} \mathop{\vtop{\ialign{... ...ckrel{q}{\wedge} G^{-1} ({\underline z}) \Bigr) } \end{array}$$ (5)

Puesto que $\stackrel{q}{\wedge} G^{-1}$ es una isometría de $\stackrel{p}{\wedge} E^*$ sobre $\stackrel{p}{\wedge} E$ y $\stackrel{q}{\wedge} G^{-1}$ es una isometría de $\stackrel{q}{\wedge} E^*$ sobre $\stackrel{q}{\wedge} E$, podemos quitar las potencias exteriores de $G^{-1}$ del segundo miembro de (5). La fórmula (5) se transforma en:

$$\$$

$$= \sum_{H \subset [\![ 1,p+q]\!] \atop \vert H\vert=p} \rho_{H, H^\... ...line x}^H \vert{\underline y}) ({\underline x}^{H^\prime} \vert {\underline z})$$ (6)

Al comparar (5) con (6) obtenemos la fórmula del enunciado. $\quad\Box$
Siguiente: El operador de Hodge Arriba: Álgebra exterior sobre un Anterior: Producto escalar canónico en