- Sea
 un espacio afín real y sean
un espacio afín real y sean 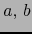 puntos de
puntos de  . El conjunto:
. El conjunto:
![\begin{displaymath}\fbox{${\displaystyle {[a,b]}= \colon \left\{ a + t(b-a) \bigm\vert 0 \le t \le 1 \right\}}$}\end{displaymath}](img2978.png)
se llama SEGMENTO DE EXTREMOS en
en  .
.
- Un subconjunto
 de
de  se llama CONJUNTO CONVEXO en
se llama CONJUNTO CONVEXO en  , si
rige la implicación:
, si
rige la implicación:
![\begin{displaymath}\fbox{${\displaystyle a,b \in {\cal S} \Rightarrow [a,b] \subset {\cal S}}$}\end{displaymath}](img2979.png)
Observación 1
Sea ![]() un subespacio maximal de un espacio vectorial
un subespacio maximal de un espacio vectorial ![]() . Puesto que
. Puesto que ![]() existe
existe ![]() tal
que
tal
que
![]() . El subespacio
. El subespacio
![]() de
de ![]() engendrado por el conjunto
engendrado por el conjunto
![]() contiene a
contiene a ![]() propiamente, luego coincide con
propiamente, luego coincide con ![]() . En otras palabras, todo vector de
. En otras palabras, todo vector de ![]() se expresa
únicamente en la forma:
se expresa
únicamente en la forma:
Pero todo punto del hiperplano ![]() se representa únicamente en la forma
se representa únicamente en la forma ![]() con
con ![]() .
.
Así pues, todo punto de ![]() se escribe únicamente como
se escribe únicamente como ![]() con
con ![]() y
y
![]() .
.
Observación 2
Con las notaciones de la observación 1, el complemento de ![]() en
en ![]() es
la reunión de dos conjuntos ajenos
es
la reunión de dos conjuntos ajenos ![]() y
y
![]() donde:
donde:
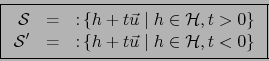
Demostración
Los conjuntos ![]() y
y
![]() son, pues, convexos.
son, pues, convexos.
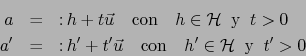
De (35) se ve que ![]() si y sólo si
si y sólo si
![]() .
Este
.
Este ![]() satisface
satisface ![]() , luego el segmento
, luego el segmento ![]() interseca
interseca
![]() en un punto.
en un punto.
![]()
Observación 3.
En el conjunto
![]() definamos una relación ``
definamos una relación ``![]() '' por
'' por