




Siguiente: Aplicaciones lineales continuas
Arriba: Preliminares geométricos y de
Anterior: Semiespacios
En este libro damos por conocidos los elementos de la teoría de espacios vectoriales normados. Para referencia
precisa, recordaremos unas definiciones fundamentales y enunciaremos sin prueba
una serie de resultados en forma de teoremas numerados.
El lector que lo desee encontrará demostraciones completas por ejemplo en
el primer tomo del tratado de Análisis de J. DIEUDONNÉ [13].
Sea  un espacio vectorial sobre
un espacio vectorial sobre  .
Una aplicación
.
Una aplicación
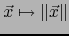 de E en
de E en 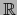 se llama una
NORMA sobre
se llama una
NORMA sobre  , si satisface:
La desigualdad del triángulo equivale a la desigualdad:
, si satisface:
La desigualdad del triángulo equivale a la desigualdad:
que llamaremos la COMPAÑERA DE LA DESIGUALDAD DEL TRIÁNGULO.
Si 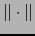 es una norma sobre
es una norma sobre  , el par
, el par 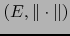 se llama un ESPACIO VECTORIAL NORMADO. Por un abuso usual de lenguaje, se dice también simplemente que
se llama un ESPACIO VECTORIAL NORMADO. Por un abuso usual de lenguaje, se dice también simplemente que  es un
espacio vectorial normado.
es un
espacio vectorial normado.
Si  se reduce al cuerpo
se reduce al cuerpo  , convenimos en usar como norma sobre él, el valor absoluto (o módulo) en
, convenimos en usar como norma sobre él, el valor absoluto (o módulo) en  .
.
Con las notaciones de arriba pongamos:
La función
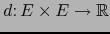 así definida es una distancia sobre el conjunto
así definida es una distancia sobre el conjunto  . Hace
de
. Hace
de  un espacio métrico, caso particular de un espacio topológico.
un espacio métrico, caso particular de un espacio topológico.
Teorema 2.1
Sea 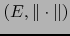 un espacio vectorial normado. Las aplicaciones
un espacio vectorial normado. Las aplicaciones
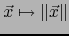 de E
en
de E
en 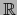 ;
;
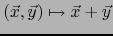 de
de 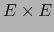 en
en  ;
;
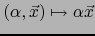 de
de
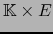 en E son aplicaciones continuas.
en E son aplicaciones continuas.
Definición 2.1
Dos normas
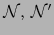 sobre un mismo espacio vectorial
sobre un mismo espacio vectorial  se dicen NORMAS EQUIVALENTES, si definen la misma topología sobre
se dicen NORMAS EQUIVALENTES, si definen la misma topología sobre  .
.
Teorema 2.2
Dos normas
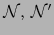 sobre un mismo espacio vectorial
sobre un mismo espacio vectorial  son
normas equivalentes si y sólo si existen números
son
normas equivalentes si y sólo si existen números 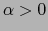 y
y 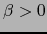 tales que:
o sea
tales que:
o sea
Corolario 2.1
Si 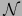 y
y
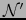 son normas equivalentes sobre
son normas equivalentes sobre  :
:
- Las aplicaciones uniformemente continuas de dominio
 o contradominio
o contradominio  son
las mismas para
son
las mismas para 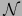 y
y
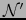 .
.
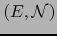 es un espacio métrico completo si y sólo si lo es
es un espacio métrico completo si y sólo si lo es
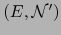 .
.
- Un subconjunto de
 es acotado para
es acotado para 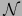 si y sólo si es acotado para
si y sólo si es acotado para
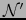 .
.
Por contraste se puede probar que si  es un espacio vectorial de dimensión infinita, hay
siempre normas inequivalentes sobre
es un espacio vectorial de dimensión infinita, hay
siempre normas inequivalentes sobre  .
.
Definición 2.2
Un espacio vectorial normado 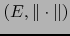 se llama ESPACIO DE BANACH, si (para la distancia definida
por la norma
se llama ESPACIO DE BANACH, si (para la distancia definida
por la norma 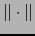 ) es un espacio métrico completo.
) es un espacio métrico completo.
Nota
STEFAN BANACH (1892-1945), gran matemático polaco, fue uno de los pioneros del análisis
matemático de este siglo, específicamente del ``análisis funcional''.
Teorema 2.4
Todo espacio vectorial normado de dimensión finita es un espacio de Banach.
Por contraste, un espacio vectorial normado de dimensión infinita puede ser completo o no.
Corolario 2.2 (del teorema
4.2.4)
Un subespacio de dimensión finita de un espacio
vectorial normado  es siempre cerrado en
es siempre cerrado en  .
.
Por contraste, un subespacio de dimensión infinita de E puede ser cerrado o no en E.
Subsections





Siguiente: Aplicaciones lineales continuas
Arriba: Preliminares geométricos y de
Anterior: Semiespacios
Guillermo M. Luna
2009-06-14


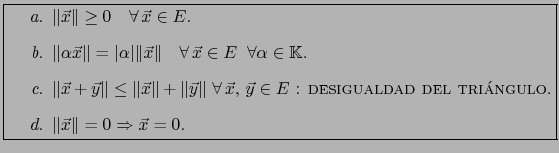
![]() es una norma sobre
es una norma sobre ![]() , el par
, el par ![]() se llama un ESPACIO VECTORIAL NORMADO. Por un abuso usual de lenguaje, se dice también simplemente que
se llama un ESPACIO VECTORIAL NORMADO. Por un abuso usual de lenguaje, se dice también simplemente que ![]() es un
espacio vectorial normado.
es un
espacio vectorial normado.
![]() se reduce al cuerpo
se reduce al cuerpo ![]() , convenimos en usar como norma sobre él, el valor absoluto (o módulo) en
, convenimos en usar como norma sobre él, el valor absoluto (o módulo) en ![]() .
.