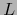 es continua.
es continua.
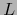 es continua en el punto cero de
es continua en el punto cero de  .
.
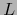 es acotada en una bola de centro
es acotada en una bola de centro 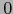 de
de  .
.
- Existe
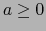 tal que:
tal que:
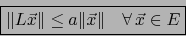
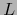 es uniformemente continua.
es uniformemente continua.
![[*]](footnote.png) el conjunto de todas las aplicaciones lineales continuas de
el conjunto de todas las aplicaciones lineales continuas de
También se ve fácilmente que ![]() admite definiciones alternativas:
admite definiciones alternativas: