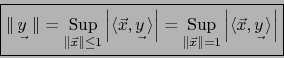Siguiente: Producto de espacios vectoriales
Arriba: Espacios vectoriales normados y
Anterior: Aplicaciones lineales continuas
I. El espacio
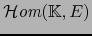
Sea  un espacio vectorial normado sobre
un espacio vectorial normado sobre  . Puesto que
. Puesto que  es un
espacio vectorial de dimensión 1 sobre sí mismo, se tiene en virtud del teorema 4.2.5:
es un
espacio vectorial de dimensión 1 sobre sí mismo, se tiene en virtud del teorema 4.2.5:
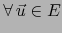 sea
sea
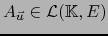 la aplicación
la aplicación
El isomorfismo lineal
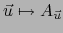 de
de  sobre
sobre
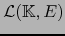 ya considerado en el
teorema 2.25 preserva las normas, pues, por la fórmula (2) después de las definiciones
4.2.3, vale:
ya considerado en el
teorema 2.25 preserva las normas, pues, por la fórmula (2) después de las definiciones
4.2.3, vale:
Se dice que dicho isomorfismo es una ISOMETR´iA LINEAL de  sobre el espacio
sobre el espacio
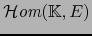 . Permite identificar
dichos espacios normados. Lo indicamos escribiendo:
. Permite identificar
dichos espacios normados. Lo indicamos escribiendo:
La isometría inversa es:
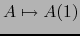
II. El espacio
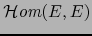
Sea  un espacio vectorial normado. Consideramos el espacio vectorial normado
un espacio vectorial normado. Consideramos el espacio vectorial normado
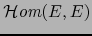 constituído por
los endomorfismos lineales continuos de
constituído por
los endomorfismos lineales continuos de  . La ``multiplicación''
. La ``multiplicación''
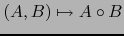 hace
de
hace
de
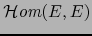 un álgebra (asociativa y unífera). El elemento uno de esta álgebra es la identidad
un álgebra (asociativa y unífera). El elemento uno de esta álgebra es la identidad
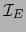 .
.
III. El espacio
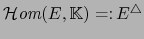
Sea  un espacio vectorial normado. El espacio vectorial normado
un espacio vectorial normado. El espacio vectorial normado
cuyos
elementos son las formas lineales continuas sobre  , se llama el DUAL TOPOLÓGICO de
, se llama el DUAL TOPOLÓGICO de  .
.
Si
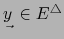 vale según las fórmulas (1), (2) en las definiciones 4.2.3,
vale según las fórmulas (1), (2) en las definiciones 4.2.3,
y también:
Teorema 2.12
Sean 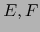 espacios vectoriales normados. Si
espacios vectoriales normados. Si 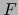 es un espacio de Banach, también el espacio vectorial
normado
es un espacio de Banach, también el espacio vectorial
normado
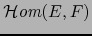 es un espacio de Banach.
es un espacio de Banach.
Por ejemplo, si E es un espacio vectorial normado completo o no, su dual topológico
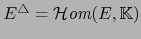 es
siempre un espacio de Banach, pues
es
siempre un espacio de Banach, pues  ( es decir
( es decir 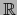 o
o 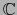 ) es un espacio métrico completo.
) es un espacio métrico completo.





Siguiente: Producto de espacios vectoriales
Arriba: Espacios vectoriales normados y
Anterior: Aplicaciones lineales continuas
Guillermo M. Luna
2009-06-14
![]()
![]() un espacio vectorial normado sobre
un espacio vectorial normado sobre ![]() . Puesto que
. Puesto que ![]() es un
espacio vectorial de dimensión 1 sobre sí mismo, se tiene en virtud del teorema 4.2.5:
es un
espacio vectorial de dimensión 1 sobre sí mismo, se tiene en virtud del teorema 4.2.5:
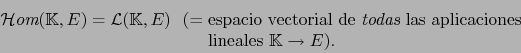
![]()
![]() un espacio vectorial normado. Consideramos el espacio vectorial normado
un espacio vectorial normado. Consideramos el espacio vectorial normado
![]() constituído por
los endomorfismos lineales continuos de
constituído por
los endomorfismos lineales continuos de ![]() . La ``multiplicación''
. La ``multiplicación''
![]() hace
de
hace
de
![]() un álgebra (asociativa y unífera). El elemento uno de esta álgebra es la identidad
un álgebra (asociativa y unífera). El elemento uno de esta álgebra es la identidad
![]() .
.
![]()
![]() un espacio vectorial normado. El espacio vectorial normado
un espacio vectorial normado. El espacio vectorial normado ![]() vale según las fórmulas (1), (2) en las definiciones 4.2.3,
vale según las fórmulas (1), (2) en las definiciones 4.2.3,