




Siguiente: Espacios afines normados
Arriba: Espacios vectoriales normados y
Anterior: Unos espacios particulares
Empecemos por recordar un concepto algebraico. Sean 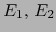 espacios vectoriales sobre un cuerpo
conmutativo
espacios vectoriales sobre un cuerpo
conmutativo  . Consideramos el producto cartesiano
. Consideramos el producto cartesiano
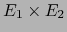 conjunto de todos los
pares
conjunto de todos los
pares
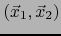 con
con
 . Si
. Si
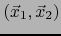 e
e
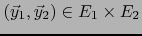 definimos:
definimos:
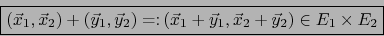 |
(4) |
Si
 y
y
 definimos:
definimos:
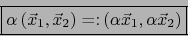 |
(5) |
Las definiciones (4) y (5) hacen de
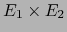 un espacio vectorial sobre
un espacio vectorial sobre  que se
llama PRODUCTO DEL ESPACIO VECTORIAL POR EL ESPACIO VECTORIAL .
que se
llama PRODUCTO DEL ESPACIO VECTORIAL POR EL ESPACIO VECTORIAL .
El espacio vectorial
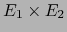 es suma directa de sus subespacios
es suma directa de sus subespacios
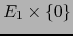 y
y
 .
.
En efecto:
- Todo elemento de
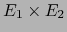 puede escribirse:
puede escribirse:
donde
 y
y
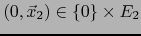 .
.
- La intersección de los subespacios
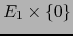 y
y
 es el elemento
cero de
es el elemento
cero de
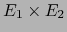 .
.
a) y b) prueban lo aseverado.
Por otra parte, la aplicación
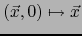 es un isomorfismo
lineal canónico de
es un isomorfismo
lineal canónico de
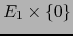 sobre
sobre 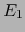 y
y
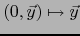 es un
isomorfismo lineal de
es un
isomorfismo lineal de
 sobre
sobre 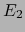 . Si, mediante dichos
isomorfismos canónicos, identificamos el espacio vectorial
. Si, mediante dichos
isomorfismos canónicos, identificamos el espacio vectorial
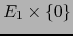 con
con 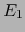 y
el espacio vectorial
y
el espacio vectorial
 con
con 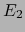 , podemos escribir:
, podemos escribir:
En particular si 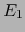 y
y 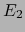 son espacios vectoriales de dimensiones finitas, tendremos:
son espacios vectoriales de dimensiones finitas, tendremos:
Volvamos al convenio:
Sean
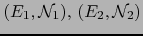 espacios vectoriales normados. Definamos una función
espacios vectoriales normados. Definamos una función
 por:
por:
Afirmamos que  es una norma sobre el espacio vectorial
es una norma sobre el espacio vectorial
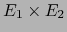 . En efecto:
. En efecto:
- Claramente
 .
.
-
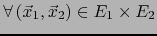 y
y
 vale:
vale:
- Para dos elementos arbitrarios
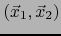 ,
,
 de
de
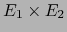 vale:
vale:
Pero
 y
y
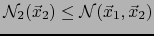 .
Así como también
.
Así como también
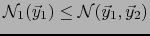 y
y
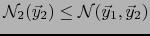 .
Así pues (6) entraña:
.
Así pues (6) entraña:
o sea, la desigualdad del triángulo para  .
.
- Supongamos
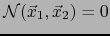 .
Ya que
.
Ya que
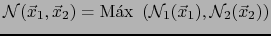 ,
la hipótesis equivale a
,
la hipótesis equivale a
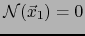 y
y
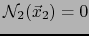 , o sea:
, o sea:
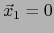 y
y 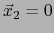 , o sea,
, o sea,
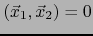 .
.
Queda pues comprobado que  es efectivamente una norma sobre el espacio vectorial
es efectivamente una norma sobre el espacio vectorial
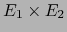 .
El espacio vectorial normado
.
El espacio vectorial normado
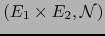 se llama el PRODUCTO DEL ESPACIO VECTORIAL NORMADO #MATH4141# POR EL
ESPACIO VECTORIAL NORMADO #MATH4142#.
se llama el PRODUCTO DEL ESPACIO VECTORIAL NORMADO #MATH4141# POR EL
ESPACIO VECTORIAL NORMADO #MATH4142#.





Siguiente: Espacios afines normados
Arriba: Espacios vectoriales normados y
Anterior: Unos espacios particulares
Guillermo M. Luna
2009-06-14
![]() espacios vectoriales sobre un cuerpo
conmutativo
espacios vectoriales sobre un cuerpo
conmutativo ![]() . Consideramos el producto cartesiano
. Consideramos el producto cartesiano
![]() conjunto de todos los
pares
conjunto de todos los
pares
![]() con
con
![]() . Si
. Si
![]() e
e
![]() definimos:
definimos:
![]() es suma directa de sus subespacios
es suma directa de sus subespacios
![]() y
y
![]() .
.
![]() es un isomorfismo
lineal canónico de
es un isomorfismo
lineal canónico de
![]() sobre
sobre ![]() y
y
![]() es un
isomorfismo lineal de
es un
isomorfismo lineal de
![]() sobre
sobre ![]() . Si, mediante dichos
isomorfismos canónicos, identificamos el espacio vectorial
. Si, mediante dichos
isomorfismos canónicos, identificamos el espacio vectorial
![]() con
con ![]() y
el espacio vectorial
y
el espacio vectorial
![]() con
con ![]() , podemos escribir:
, podemos escribir:

![]() es efectivamente una norma sobre el espacio vectorial
es efectivamente una norma sobre el espacio vectorial
![]() .
El espacio vectorial normado
.
El espacio vectorial normado
![]() se llama el PRODUCTO DEL ESPACIO VECTORIAL NORMADO
se llama el PRODUCTO DEL ESPACIO VECTORIAL NORMADO