




Siguiente: Aplicaciones afines continuas
Arriba: Espacios vectoriales normados y
Anterior: Producto de espacios vectoriales
Definición 2.4
Sea  un espacio afín sobre un espacio vectorial E. Un par
un espacio afín sobre un espacio vectorial E. Un par
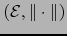 donde
donde
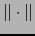 es una norma sobre el espacio vectorial E se llama ESPACIO AF´iN NORMADO. Por abuso
de lenguaje se dice que
es una norma sobre el espacio vectorial E se llama ESPACIO AF´iN NORMADO. Por abuso
de lenguaje se dice que  es un espacio afín normado.
es un espacio afín normado.
Sea  un espacio afín normado y sea
un espacio afín normado y sea 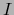 un origen arbitrario en
un origen arbitrario en  . Para todo par
. Para todo par
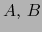 de puntos de
de puntos de  tenemos en virtud del teorema 4.1.1:
tenemos en virtud del teorema 4.1.1:
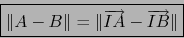 |
(7) |
Teniendo en cuenta que por el teorema 4.1.3 la aplicación
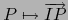 es una biyección
del espacio afín
es una biyección
del espacio afín  sobre su espacio vectorial asociado
sobre su espacio vectorial asociado  , deducimos de la fórmula (7), que
la aplicación
, deducimos de la fórmula (7), que
la aplicación
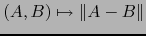 de
de
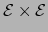 en
en 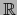 es una distancia en
es una distancia en  (que hace de
(que hace de  un espacio métrico) y la biyección
un espacio métrico) y la biyección
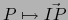 es una isometría del espacio métrico
es una isometría del espacio métrico
 sobre el espacio métrico E. La isometría inversa es la aplicación
sobre el espacio métrico E. La isometría inversa es la aplicación
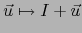 .
.
Por ser  y
y  espacios métricos isométricos, tenemos sin más:
espacios métricos isométricos, tenemos sin más:
Teorema 2.13
Un espacio afín normado  es un espacio métrico completo si y sólo si
su espacio vectorial asociado
es un espacio métrico completo si y sólo si
su espacio vectorial asociado  es un espacio de Banach.
es un espacio de Banach.
También:
Teorema 2.14
Dos normas sobre  definen la misma topología sobre el espacio afín
definen la misma topología sobre el espacio afín  si y sólo si
son normas equivalentes.
si y sólo si
son normas equivalentes.
Supongamos  (equivalentemente
(equivalentemente  ) de dimensión finita. Sabemos por el teorema
4.2.3, que entonces dos normas arbitrarias sobre
) de dimensión finita. Sabemos por el teorema
4.2.3, que entonces dos normas arbitrarias sobre  son equivalentes, luego:
son equivalentes, luego:
Los teoremas 4.2.4 y 4.2.13 entrañan:
Teorema 2.16
Todo espacio afín normado de dimensión finita es un espacio métrico completo.
Esto implica a su vez:
Teorema 2.17
Toda variedad afín de dimensión finita en un espacio afín normado  es un conjunto cerrado en
es un conjunto cerrado en  .
.
Demostración
Sea 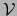 una variedad afín de dimensión finita en el espacio afín normado
una variedad afín de dimensión finita en el espacio afín normado  y
y
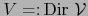 . La topología
de
. La topología
de 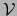 inducida por la de
inducida por la de  es la misma que aquella definida mediante la restricción a
es la misma que aquella definida mediante la restricción a 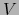 de la norma en
de la norma en  . Por el
teorema 4.2.16
. Por el
teorema 4.2.16 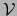 es un espacio métrico completo, luego
es un espacio métrico completo, luego 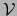 es cerrado en
es cerrado en  .
.






Siguiente: Aplicaciones afines continuas
Arriba: Espacios vectoriales normados y
Anterior: Producto de espacios vectoriales
Guillermo M. Luna
2009-06-14
![]() un espacio afín normado y sea
un espacio afín normado y sea ![]() un origen arbitrario en
un origen arbitrario en ![]() . Para todo par
. Para todo par
![]() de puntos de
de puntos de ![]() tenemos en virtud del teorema 4.1.1:
tenemos en virtud del teorema 4.1.1:
![]() y
y ![]() espacios métricos isométricos, tenemos sin más:
espacios métricos isométricos, tenemos sin más:
![]() una variedad afín de dimensión finita en el espacio afín normado
una variedad afín de dimensión finita en el espacio afín normado ![]() y
y
![]() . La topología
de
. La topología
de ![]() inducida por la de
inducida por la de ![]() es la misma que aquella definida mediante la restricción a
es la misma que aquella definida mediante la restricción a ![]() de la norma en
de la norma en ![]() . Por el
teorema 4.2.16
. Por el
teorema 4.2.16 ![]() es un espacio métrico completo, luego
es un espacio métrico completo, luego ![]() es cerrado en
es cerrado en ![]() .
.
![]()