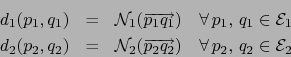Siguiente: Diferenciación en espacios afines
Arriba: Espacios vectoriales normados y
Anterior: Aplicaciones afines continuas
Empecemos por un concepto algebraico. Sean
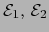 espacios afines
sobre un cuerpo conmutativo arbitrario
espacios afines
sobre un cuerpo conmutativo arbitrario  y sean
y sean 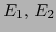 sus sendos espacios vectoriales asociados.
Consideremos el producto cartesiano
sus sendos espacios vectoriales asociados.
Consideremos el producto cartesiano
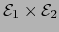 , conjunto de todos los pares
, conjunto de todos los pares 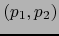 con
con
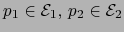 .
.
Si
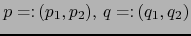 son elementos arbitrarios de
son elementos arbitrarios de
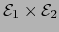 , definimos el
vector
, definimos el
vector
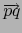 del espacio vectorial producto
del espacio vectorial producto
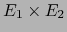 por:
por:
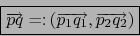 |
(8) |
Afirmamos que la definición (8) hace de
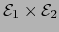 un espacio afín sobre el espacio vectorial
un espacio afín sobre el espacio vectorial
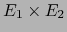 . En efecto:
. En efecto:
- Supongamos
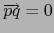 , equivalentemente:
, equivalentemente:
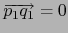 y
y
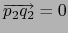 . Esto implica
. Esto implica
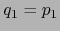 y
y 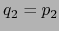 , o sea,
, o sea, 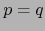 .
.
- Sean
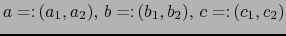 tres elementos
arbitrarios de
tres elementos
arbitrarios de
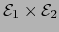 . Vale:
. Vale:
Se verifica, pues, la relación de Chasles en
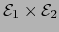 .
.
- Sean dados
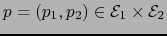 y
y
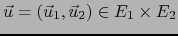 arbitrarios. Existen puntos
arbitrarios. Existen puntos
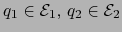 tales que:
tales que:
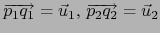 . Para
. Para
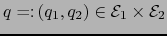 , vale:
, vale:
Se cumplen, pues, los axiomas de los espacios afines para el conjunto
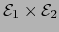 y el espacio
vectorial
y el espacio
vectorial
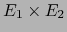 .
.
El espacio afín
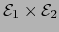 , de espacio vectorial asociado
, de espacio vectorial asociado
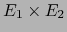 se llama el
PRODUCTO DEL ESPACIO VECTORIAL AF´iN POR EL ESPACIO VECTORIAL AF´iN .
se llama el
PRODUCTO DEL ESPACIO VECTORIAL AF´iN POR EL ESPACIO VECTORIAL AF´iN .
Volvemos al convenio:
Sean
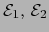 espacios afines normados. Los espacios vectoriales asociados correspondientes
espacios afines normados. Los espacios vectoriales asociados correspondientes
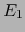 y
y 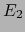 están provistos de sendas normas
están provistos de sendas normas
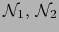 y por consiguiente,
el espacio vectorial producto
y por consiguiente,
el espacio vectorial producto
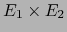 de la norma
de la norma 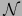 dada por:
dada por:
luego
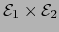 es un espacio afín normado.
Se llama el PRODUCTO DEL ESPACIO VECTORIAL AF´iN NORMADO POR EL ESPACIO VECTORIAL AF´iN NORMADO .
es un espacio afín normado.
Se llama el PRODUCTO DEL ESPACIO VECTORIAL AF´iN NORMADO POR EL ESPACIO VECTORIAL AF´iN NORMADO .
Observación
Sean 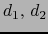 las distancias en sendos espacios
las distancias en sendos espacios
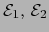 y
y 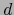 la distancia inducida en
la distancia inducida en
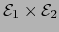 . Vale:
. Vale:
luego:
o sea:
Así pues, el espacio métrico
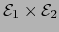 es el producto de los espacios métricos
es el producto de los espacios métricos
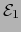 y
y 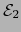 . También el espacio topológico
. También el espacio topológico
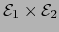 es el producto de los
espacios topológicos
es el producto de los
espacios topológicos 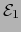 y
y 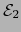 .
.





Siguiente: Diferenciación en espacios afines
Arriba: Espacios vectoriales normados y
Anterior: Aplicaciones afines continuas
Guillermo M. Luna
2009-06-14
![]() espacios afines
sobre un cuerpo conmutativo arbitrario
espacios afines
sobre un cuerpo conmutativo arbitrario ![]() y sean
y sean ![]() sus sendos espacios vectoriales asociados.
Consideremos el producto cartesiano
sus sendos espacios vectoriales asociados.
Consideremos el producto cartesiano
![]() , conjunto de todos los pares
, conjunto de todos los pares ![]() con
con
![]() .
.
![]() son elementos arbitrarios de
son elementos arbitrarios de
![]() , definimos el
vector
, definimos el
vector
![]() del espacio vectorial producto
del espacio vectorial producto
![]() por:
por:
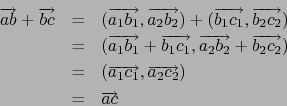
![]() las distancias en sendos espacios
las distancias en sendos espacios
![]() y
y ![]() la distancia inducida en
la distancia inducida en
![]() . Vale:
. Vale: