




Siguiente: Producto de espacios afines
Arriba: Espacios vectoriales normados y
Anterior: Espacios afines normados
Sean
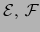 espacios afines normados de sendos espacios vectoriales asociados
espacios afines normados de sendos espacios vectoriales asociados  y
y 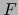 .
.
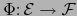 una aplicación afín. Escribiendo:
una aplicación afín. Escribiendo:
vemos inmediatamente que 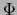 es continua en cualquier punto
es continua en cualquier punto 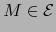 si y sólo si
si y sólo si 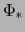 es continua en el punto cero.
De ahí:
es continua en el punto cero.
De ahí:
Teorema 2.18
La aplicación afín 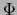 es continua, si es continua en un punto de
es continua, si es continua en un punto de  .
.
Del teorema 4.2.5 (enunciado b)) fluye también:
Teorema 2.19
La aplicación afín
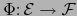 es continua si y sólo si
su parte lineal
es continua si y sólo si
su parte lineal 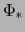 es una aplicación lineal continua de
es una aplicación lineal continua de  en
en 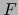 .
.
Junto con el teorema 4.2.6 esto trae consigo:
Teorema 2.20
Si  es un espacio afín normado de dimensión finita, toda aplicación afín
es un espacio afín normado de dimensión finita, toda aplicación afín
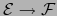 es continua.
es continua.
Finalmente vale:
Teorema 2.21
Si
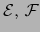 son espacios afines normados, toda aplicación afín continua
son espacios afines normados, toda aplicación afín continua
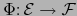 es uniformemente
continua.
es uniformemente
continua.
Esto se sigue de la fórmula:
y de que 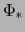 es continua en el punto cero.
es continua en el punto cero.





Siguiente: Producto de espacios afines
Arriba: Espacios vectoriales normados y
Anterior: Espacios afines normados
Guillermo M. Luna
2009-06-14
![]() espacios afines normados de sendos espacios vectoriales asociados
espacios afines normados de sendos espacios vectoriales asociados ![]() y
y ![]() .
.
![]() una aplicación afín. Escribiendo:
una aplicación afín. Escribiendo: