




Siguiente: Atlas maximales
Arriba: Mapas y atlas admisibles.
Anterior: Mapas y atlas admisibles.
Sean
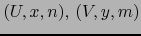 mapas de un espacio topológico
mapas de un espacio topológico 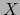 tales que sus dominios sean ajenos,
tales que sus dominios sean ajenos,
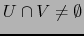 .
.
Si consideramos las aplicaciones 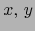 restringidas al abierto
restringidas al abierto 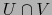 de
de 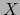 la aplicación:
la aplicación:
será un homeomorfismo del abierto 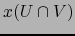 de
de
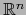 sobre el
abierto
sobre el
abierto 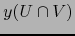 de
de
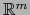 . Del teorema de la invariancia de la
dimensión se sigue
. Del teorema de la invariancia de la
dimensión se sigue 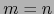 . Así pues,:
. Así pues,:
Teorema 1.5
Si los dominios de dos mapas de un espacio topológico se intersecan, las
dimensiones de ambos mapas son iguales.
El homeomorfismo
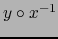 de
de 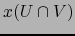 sobre
sobre 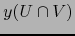 y su
inverso
y su
inverso
 , homeomorfismo de
, homeomorfismo de 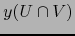 sobre
sobre 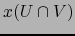 se llaman CAMBIOS DE MAPAS.
se llaman CAMBIOS DE MAPAS.
Definición 1.2
Sean  una variedad topológica y
una variedad topológica y  un punto de
un punto de  . Si
. Si 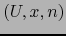 es
un mapa de
es
un mapa de  en el punto
en el punto  definimos la DIMENSIÓN DE LA VARIEDAD
definimos la DIMENSIÓN DE LA VARIEDAD  en el punto
en el punto  como
como
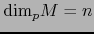 .
.
En virtud del teorema 5.1.5 esta definición es unívoca, o sea es
independiente del mapa 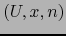 elegido en el punto
elegido en el punto  de
de  .
Con las notaciones de la definición 5.1.2 tenemos claramente
.
Con las notaciones de la definición 5.1.2 tenemos claramente
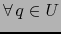 :
:
 .
De esto se sigue que
.
De esto se sigue que
 el conjunto:
el conjunto:
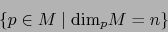 |
(1) |
es una vecindad de cualquiera de sus puntos, es decir es un
conjunto abierto.
El complemento del conjunto (1) es:
Dicho complemento, reunión de conjuntos abiertos, es también un
conjunto abierto. De ahí vemos: Una variedad topológica conexa tiene
la misma dimensión en todo punto.
Definición 1.3
Una variedad topológica  se dice VARIEDAD PURA si tiene la misma
dimensión en todo punto. Dicha dimensión se llama la DIMENSIÓN DE LA VARIEDAD
se dice VARIEDAD PURA si tiene la misma
dimensión en todo punto. Dicha dimensión se llama la DIMENSIÓN DE LA VARIEDAD  .
.
Acabamos de probar:
Toda variedad topológica conexa es una variedad pura.
Recordemos que un espacio topológico 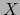 es localmente conexo si y sólo
si las componentes conexas de todo abierto de
es localmente conexo si y sólo
si las componentes conexas de todo abierto de 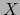 son también conjuntos
abiertos. En particular, toda componente conexa de
son también conjuntos
abiertos. En particular, toda componente conexa de 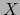 es un conjunto abierto
(y también cerrado) en
es un conjunto abierto
(y también cerrado) en 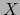 .
De ahí , sin más, por el teorema 5.1.1:
.
De ahí , sin más, por el teorema 5.1.1:
Teorema 1.6
Las componentes conexas de toda variedad topológica  son conjuntos a
la vez abiertos y cerrados en
son conjuntos a
la vez abiertos y cerrados en  .
Luego
.
Luego  es la suma topológica de sus componentes conexas.
es la suma topológica de sus componentes conexas.
Sean 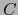 una componente conexa de
una componente conexa de  y
y 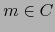 . Sea
. Sea 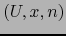 un mapa de
la variedad
un mapa de
la variedad  en el punto
en el punto  . Ya que
. Ya que 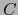 es un abierto de
es un abierto de  ,
, 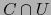 es un abierto tanto en
es un abierto tanto en  como en
como en 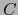 y
y
 es un mapa de
es un mapa de 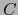 en
en  .
. 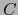 es, pues, también una variedad topológica y, por
lo visto arriba, es una variedad pura. Así pues, el teorema 5.1.6
entraña:
es, pues, también una variedad topológica y, por
lo visto arriba, es una variedad pura. Así pues, el teorema 5.1.6
entraña:
Teorema 1.7
Toda variedad topológica es suma topológica de variedades puras.
Sin pérdida esencial de generalidad podemos, pues, limitarnos a estudiar
variedades puras.
Esto ocurrirá en particular, si la variedad de que se trata es pura o
si la dimensión no interesa mayormente. Frecuentemente se estará dado
implícitamente cuando escribamos
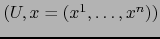 .
.
Las variedades topológicas no poseen una estructura suficientemente rica para
servir de sede a un cálculo diferencial. Para ello necesitamos objetos
matemáticos con estructura más precisa, llamados ``variedades diferenciables''.
Éstas nos proponemos ahora definir y estudiar.
Aunque variedades diferenciables sean un caso particular de
variedades topológicas, su teoría, es decir de hecho todo nuestro libro,
será independiente de los teoremas de Brouwer. En efecto para las
variedades diferenciables el teorema 5.1.5 y sus consecuencias
los teoremas 5.1.6 y 5.1.7 se seguirán sin más del corolario del teorema 4.4.5.
Los teoremas de Brouwer los citamos meramente como complemento ``inoficial'' de
información para el lector.
Definición 1.4
Sean
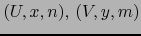 dos mapas de un espacio topológico
dos mapas de un espacio topológico 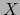 (a
suponer que existen). Sea
(a
suponer que existen). Sea
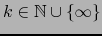 . Se dice
que los mapas considerados son COMPATIBLES
. Se dice
que los mapas considerados son COMPATIBLES  si bien
si bien
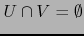 o bien
o bien
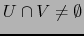 y el cambio de mapa
y el cambio de mapa
 es una aplicación de clase
es una aplicación de clase  en el abierto
en el abierto 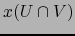 de
de
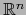 .
.
Invirtiendo los papeles de los dos mapas, vemos que si los mapas
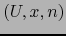 ,
, 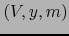 son compatibles
son compatibles  y
y
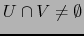 ,
también el cambio de mapa
,
también el cambio de mapa  es de clase
es de clase  en el abierto
en el abierto
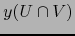 de
de
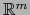 . A fin de cuentas
. A fin de cuentas
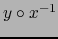 es un
isomorfismo
es un
isomorfismo  del abierto
del abierto 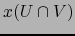 de
de
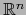 sobre el abierto
sobre el abierto
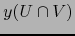 de
de
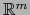 .
.
De ahí, por el corolario del teorema 4.4.5 y, sin uso de los
teoremas de Brouwer:
Definición 1.5
- Un atlas
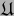 sobre un espacio topológico
sobre un espacio topológico 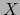 (a suponer que existe) se dice ATLAS COHERENTE
(a suponer que existe) se dice ATLAS COHERENTE  si todo par de
mapas de
si todo par de
mapas de 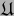 es compatible
es compatible  .
.
- Sean
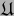 ,
, 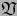 dos atlas coherentes
dos atlas coherentes  sobre
sobre 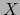 . Dichos atlas se dicen ATLAS EQUIVALENTES, y se escribe
. Dichos atlas se dicen ATLAS EQUIVALENTES, y se escribe
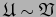 ,
si
,
si
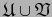 es un atlas coherente
es un atlas coherente  .
Vale decir, todo mapa de
.
Vale decir, todo mapa de 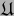 es compatible
es compatible  con todo mapa
de
con todo mapa
de 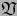 .
.
Lema 1.1
Sean  ,
, 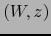 mapas de un espacio topológico
mapas de un espacio topológico 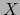 . Se supone
que cada uno de dichos mapas es compatible
. Se supone
que cada uno de dichos mapas es compatible  con todo mapa de cierto
atlas
con todo mapa de cierto
atlas 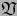 de
de 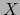 .
Entonces dichos mapas son compatibles
.
Entonces dichos mapas son compatibles  entre sí.
entre sí.
Demostración
Basta suponer
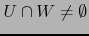 . Con esta hipótesis debemos probar
que el cambio de mapa
. Con esta hipótesis debemos probar
que el cambio de mapa
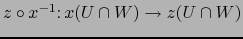 es una aplicación de clase
es una aplicación de clase  . En virtud del teorema 4.50 (``carácter
local de aplicaciones de clase
. En virtud del teorema 4.50 (``carácter
local de aplicaciones de clase  '') basta mostrar que todo punto del
abierto
'') basta mostrar que todo punto del
abierto 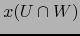 posee una vecindad abierta contenida en
posee una vecindad abierta contenida en 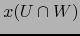 tal que la restricción de
tal que la restricción de
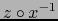 a dicha vecindad abierta es de
clase
a dicha vecindad abierta es de
clase  .
.
Aprovechando el hecho de que la restricción de  al abierto
al abierto 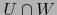 de
de 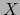 es un homeomorfismo de
es un homeomorfismo de 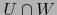 sobre
sobre 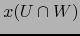 , podemos formular
esta condición como sigue:
, podemos formular
esta condición como sigue:
 |
(2) |
Sea, pues,  un punto arbitrario de
un punto arbitrario de 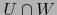 . Sea
. Sea  un mapa del
atlas
un mapa del
atlas 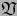 en el punto
en el punto  . Definamos:
. Definamos:
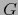 es una vecindad abierta del punto
es una vecindad abierta del punto  en
en 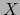 contenida en el abierto
contenida en el abierto
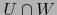 de
de 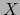 .
Vale:
.
Vale:
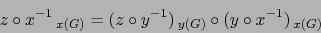 |
(3) |
Ahora bien, por hipótesis los mapas  y
y 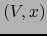 son compatibles
son compatibles
 , es decir, la aplicación
, es decir, la aplicación
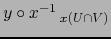 es de
clase
es de
clase  en
en 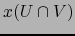 . Por el teorema 4.5.6 también su restricción
. Por el teorema 4.5.6 también su restricción
 es de clase
es de clase  en
en  .
.
Igualmente, por hipótesis los mapas  y
y 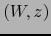 son compatibles
son compatibles  ,
es decir, la aplicación
,
es decir, la aplicación
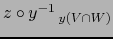 es de clase
es de clase  .
También su restricción
.
También su restricción
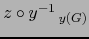 es de clase
es de clase  .
Se sigue, pues, de (3) en virtud del teorema 4.5.5 que la aplicación
.
Se sigue, pues, de (3) en virtud del teorema 4.5.5 que la aplicación
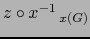 es de clase
es de clase  .
.
Con ello vienen probados la afirmación (2) y el lema.

Teorema 1.8
La relación  de la definición 5.1.5 es una relación de
equivalencia en el conjunto de todos los atlas coherentes
de la definición 5.1.5 es una relación de
equivalencia en el conjunto de todos los atlas coherentes  sobre un
espacio topológico
sobre un
espacio topológico 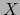 .
.
Demostración
La relación  es obviamente reflexiva y simétrica. En virtud del
lema 5.1.1 es también transitiva.
es obviamente reflexiva y simétrica. En virtud del
lema 5.1.1 es también transitiva.

Del lema 5.1.1 se sigue:
Un mapa admisible de una variedad  es compatible
es compatible  con
todo mapa de un atlas admisible cualquiera de dicha variedad
con
todo mapa de un atlas admisible cualquiera de dicha variedad  .
.
Por un abuso del lenguaje común de tipo ya varias veces señalado se
habla simplemente de la ``variedad  de clase
de clase  '' en vez de la
variedad
'' en vez de la
variedad
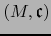 de clase
de clase  . Evidentemente no es
lícito comentar dicho abuso de lenguaje, si se considera diferentes
estructuras de variedad diferenciable sobre el mismo espacio topológico
. Evidentemente no es
lícito comentar dicho abuso de lenguaje, si se considera diferentes
estructuras de variedad diferenciable sobre el mismo espacio topológico
 .
.
Como secuela de dicho abuso de lenguaje se habla de ``atlas admisibles'' y de
``mapas admisibles'' de la ``variedad  de clase
de clase  ''.
''.
Si
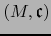 es una variedad
es una variedad  , el espacio topológico
, el espacio topológico  es patentemente una variedad topológica. Permitiéndonos el abuso de
lenguaje mencionado, diremos que toda variedad diferenciable es a
fortiori una variedad topológica.
es patentemente una variedad topológica. Permitiéndonos el abuso de
lenguaje mencionado, diremos que toda variedad diferenciable es a
fortiori una variedad topológica.
Valen, pues, para una variedad diferenciable los teoremas desde
5.1.1 hasta 5.1.7 inclusive. Como ya dicho, los teoremas
5.1.5, 5.1.6, 5.1.7 para vecindades diferenciables son independientes de
los teoremas de Brouwer.





Siguiente: Atlas maximales
Arriba: Mapas y atlas admisibles.
Anterior: Mapas y atlas admisibles.
Guillermo M. Luna
2009-06-14
![]() mapas de un espacio topológico
mapas de un espacio topológico ![]() tales que sus dominios sean ajenos,
tales que sus dominios sean ajenos,
![]() .
.
![]() restringidas al abierto
restringidas al abierto ![]() de
de ![]() la aplicación:
la aplicación:


![]() . Con esta hipótesis debemos probar
que el cambio de mapa
. Con esta hipótesis debemos probar
que el cambio de mapa
![]() es una aplicación de clase
es una aplicación de clase ![]() . En virtud del teorema 4.50 (``carácter
local de aplicaciones de clase
. En virtud del teorema 4.50 (``carácter
local de aplicaciones de clase ![]() '') basta mostrar que todo punto del
abierto
'') basta mostrar que todo punto del
abierto ![]() posee una vecindad abierta contenida en
posee una vecindad abierta contenida en ![]() tal que la restricción de
tal que la restricción de
![]() a dicha vecindad abierta es de
clase
a dicha vecindad abierta es de
clase ![]() .
.
![]() al abierto
al abierto ![]() de
de ![]() es un homeomorfismo de
es un homeomorfismo de ![]() sobre
sobre ![]() , podemos formular
esta condición como sigue:
, podemos formular
esta condición como sigue:
![]() y
y ![]() son compatibles
son compatibles ![]() ,
es decir, la aplicación
,
es decir, la aplicación
![]() es de clase
es de clase ![]() .
También su restricción
.
También su restricción
![]() es de clase
es de clase ![]() .
Se sigue, pues, de (3) en virtud del teorema 4.5.5 que la aplicación
.
Se sigue, pues, de (3) en virtud del teorema 4.5.5 que la aplicación
![]() es de clase
es de clase ![]() .
.
![]()
![]() es obviamente reflexiva y simétrica. En virtud del
lema 5.1.1 es también transitiva.
es obviamente reflexiva y simétrica. En virtud del
lema 5.1.1 es también transitiva.
![]()
![]() , automáticamente
también admisible.
, automáticamente
también admisible.
![]() es compatible
es compatible ![]() con
todo mapa de un atlas admisible cualquiera de dicha variedad
con
todo mapa de un atlas admisible cualquiera de dicha variedad ![]() .
.
![]() de clase
de clase ![]() '' en vez de la
variedad
'' en vez de la
variedad
![]() de clase
de clase ![]() . Evidentemente no es
lícito comentar dicho abuso de lenguaje, si se considera diferentes
estructuras de variedad diferenciable sobre el mismo espacio topológico
. Evidentemente no es
lícito comentar dicho abuso de lenguaje, si se considera diferentes
estructuras de variedad diferenciable sobre el mismo espacio topológico
![]() .
.
![]() de clase
de clase ![]() ''.
''.
![]() es una variedad
es una variedad ![]() , el espacio topológico
, el espacio topológico ![]() es patentemente una variedad topológica. Permitiéndonos el abuso de
lenguaje mencionado, diremos que toda variedad diferenciable es a
fortiori una variedad topológica.
es patentemente una variedad topológica. Permitiéndonos el abuso de
lenguaje mencionado, diremos que toda variedad diferenciable es a
fortiori una variedad topológica.