 es una biyección de
es una biyección de 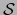 sobre
sobre 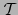 ,
,
 es diferenciable en
es diferenciable en 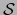 ,
,
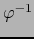 es diferenciable en
es diferenciable en 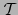 .
.
Nota
Mucho se ha difundido la bárbara palabra ``difeomorfismo'' por lo que llamamos ``isomorfismo diferenciable''. En
este libro no la usaremos.
Demostración
Las fórmulas:
Entonces si uno de los espacios
![]() es de dimensión finita, también lo es el otro y vale:
es de dimensión finita, también lo es el otro y vale:
Si ![]() es diferenciable en un punto
es diferenciable en un punto ![]() y
y ![]() es diferenciable en el punto
es diferenciable en el punto
![]() vale:
vale: