Análisis de la región compleja de la relación de dispersión.

Ahora queremos encontrar una ecuación analítica que nos describa la región compleja (Región II), de la gráfica (IV.IV).

Partiendo de la relación de dispersión descrita por (2.21), esto es:

$$\mu^4 -\gamma\mu^3 -\beta\mu^2 -\gamma\mu +1 =0$$ (4.21)

en donde hemos empleado las definiciones siguientes, descritas con anterioridad.

$$\left\{\begin{array}{ccl} \gamma & = & -\frac{a_1}{a_2} =... ...\\ \beta & = & \frac{\lambda -a_0}{a_2} \end{array}\right.$$ (4.22)

Dividiendo por $\mu^2 (\neq 0)$ la relación de dispersión, obtenemos

$$(\mu^2 +\frac{1}{\mu^2}) -\gamma(\mu +\frac{1}{\mu}) -\beta =0$$

completando un binomio cuadrado perfecto, en el primer término.

$$(\mu +\frac{1}{\mu})^2 -\gamma(\mu+\frac{1}{\mu}) -(\beta +2) = 0$$

Es conveniente reintroducir

$$C =\cosh\phi =\frac{1}{2}(\mu +\frac{1}{\mu})$$

que al sustituirlo en la ecuación anterior resulta

$$4C^2 -2\gamma C- (\beta +2) =0$$

finalmente es deseable expresar $\beta$ en términos de la frecuencia, por lo cual, trabajando en las ecuaciones (4.22) obtenemos

$$\beta = \frac{\lambda +2(a_1 +a_2)}{a_2}$$

$$= \frac{\lambda}{a_2} +2(1 -\gamma)$$ (4.23)

sin embargo, nosotros hemos normalizado la frecuencia por medio del intervalo de Gerschoring, usando como parametro $\xi$, es decir

$$\xi =-\frac{\lambda}{4(a_1 +a_2)}$$

Con lo que:

$$\lambda =-4\xi(a_1 +a_2)$$

bajo estas consideraciones (4.23), se transforma en

$$\begin{eqnarray*} \beta & = & \frac{-4\xi(a_1 +a_2)}{a_2} +2(1-\gamma) \\ & = & 2(1-\gamma)(1-2\xi) \end{eqnarray*}$$

sustituyendo todo esto en la relación de dispersión resulta

$$2C^2 -\gamma C -[(1 -\gamma)(1 -2\xi) +1] = 0$$

Poniendo finalmente $\gamma$ en términos de $Y$

$$2C^2 -4YC -[(1-4Y) (1-2\xi) + 1] = 0$$

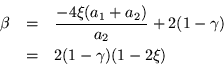
Por lo tanto tenemos una expresión para $C$ en términos de los parámetros $Y$ y $\xi$ esto es

$$C = \frac{-4Y\pm \sqrt{16Y^2 +4\cdot 2\cdot [(1+4Y)(1-2\xi)+1]}} {2\cdot 2}$$

$$= -Y\pm \sqrt{(Y+1)^2 -\xi(1+4Y)}$$ (4.24)

Como sabemos, $C$ puede ser real o complejo. Cuando es real los valores críticos son $C=\pm 1$, que ya han sido analizados, lo que interesa estudiar ahora es la región en que $C$ llega a ser compleja; cuando es compleja, la parte real es $-Y$ y la parte imaginaria es $\sqrt{\xi(1+4Y) -(Y+1)^2}$, desde luego que el único camino de que un número complejo sea tal, es de que su radical sea negativo. Por otra parte queremos trabajar con $C$ complejo, por lo cual definamos

$$C =\cosh\phi = \cosh (\alpha + i\beta)$$

$$= \cosh\alpha\cosh\beta +i\,{\mbox{senh}}\alpha\,{\mbox{senh}}\beta =a+ib$$ (4.25)

En donde:

$$\begin{eqnarray*} a & = & \cosh\alpha\cosh\beta \\ b & = & \mbox{senh}\:\alpha\:\mbox{senh}\: \beta \end{eqnarray*}$$

Entonces

$$\begin{eqnarray*} a^2 & = & \cosh^2\alpha\cos^2\beta =\cosh^2\alpha(1-\,{\mbox{... ... = -\,{\mbox{sen}}^2\beta +\cosh^2\alpha\,{\mbox{sen}}^2\beta \end{eqnarray*}$$

Despejando de estas dos ecuaciones $\,{\mbox{sen}}^2\beta$ e igualando resulta

$$\frac{b^2}{\cosh^2\alpha -1} =\frac{\cosh^2\alpha -a^2}{\cosh^2\alpha}$$

llamando a $x =\cosh^2\alpha$ a resulta

$$b^2 x=(x-1)(x-a^2)$$

Que resolviendo para $x$ resulta

$$x=\frac{a^2 +b^2 +1\pm \sqrt{(a^2 +b^2 +1)^2 -4a^2}}{2}$$ (4.26)

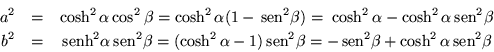
Además como hemos definido $C = a+ib$, de (4.24) resulta que

$$\left\{\begin{array}{ccl} a & = & -Y \\ b & = & \sqrt{\xi (1+4Y) -(Y+1)^2} \end{array}\right\}$$ (4.27)

Ahora vamos a encontrar la forma explícita en términos de $\xi ;\; Y$ y del descriminante de $x$, esto es.

$$a^2 +b^2 +1 = Y^2 + [\xi (1+4Y)-Y^2 -2Y - 1]+1 = \xi (1+4Y) - 2Y$$

O sea que el descriminante total tiene la forma

$$(a^2 +b^2 +1) -4a^2 = [\xi (1+4Y) -2Y]^2 -4Y^2$$

$$= \xi(1+4Y)(\xi +4\xi Y -4Y)$$ (4.28)

Desde luego que esto no tiene la apariencia de un cuadrado perfecto por lo tanto no es posible eliminar el radical, para hacerlo tomemos la expresión para $x$ dada por (4.26), junto con las dos ecuaciones anteriores y la misma definición de $x$, esto es

$$\begin{eqnarray*}[2\cosh^2\alpha +2Y -\xi (1+4Y)]^2 & = & \xi^2 (1+4Y)^2 -4\xi Y(1+4Y) \\ (Y +\cosh^2\alpha )^2 & = & \xi (1+4Y) \cosh^2\alpha \end{eqnarray*}$$

Despejando finalmente $\xi$ tenemos

$$\xi =\frac{(Y+\cosh^2\alpha)^2}{(1+4Y)\cosh^2\alpha }$$ (4.29)

En forma similar

$$\begin{eqnarray*} \cosh^2\alpha =\frac{a^2}{1-\,{\mbox{sen}}^2\beta} \\ \cosh^2\alpha =\frac{b^2}{\,{\mbox{sen}}^2\beta}+1 \end{eqnarray*}$$

Así que

$$\frac{a^2}{1-\,{\mbox{sen}}^2\beta} =\frac{b^2 +\,{\mbox{sen}}^2\beta}{\,{\mbox{sen}}^2\beta}$$

Para simplificar el álgebra llamemos $x =\,{\mbox{sen}}^2\beta$, entonces

$$xa^2 =(b^2 +x)(1-x)$$

Resolviendo para $x$, resulta

$$x =\frac{-(a^2 +b^2 -1)\pm \sqrt{(a^2 +b^2 -1)^2 +ab^2}}{2}$$ (4.30)

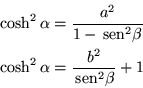
Calculemos el descriminante en términos de $\xi$ y $Y$, definidos por (4.27)

$$1-a^2 -b^2 = 1-Y^2 -[\xi (1+4Y) -(Y+1)^2 ]$$ (4.31)

$$-(a^2 +b^2 -1) = 2 +2Y -\xi(1 +4Y)$$

Por lo cual el radical tiene la forma

$$(a^2 +b^2 -1)^2 +4b^2 = [2+2Y-\xi(1+4Y)]^2 +4[\xi(1+4Y)-(Y+1)^2]$$

$$= \xi^2 (1+4Y)^2 -4Y\xi (1+4Y)$$ (4.32)

$$= \xi(1+4Y)(\xi +4\xi Y -4Y)$$

Como vemos obtenemos un resultado bastante curioso, ya que resulta la misma expresión obtenida al determinar la dependencia en $\cosh\alpha$ (ec. 4.28). Otra vez no hemos podido obtener, un cuadrado perfecto por lo cual racionalizamos la definición original de $x$, es decir, de la ecuación (4.30) tenemos

$$2\,{\mbox{sen}}^2\beta =-(a^2 +b^2 -1)+\sqrt{(a^2 +b^2 -1)^2 +4b^2}$$

Sustituyendo las ecuaciones (4.31) y (4.32) resulta

$$\begin{eqnarray*}[2\,{\mbox{sen}}^2\beta -2-2Y +\xi(1+4Y)]^2 & = & \xi^2 (1+4Y)^2 -4Y\xi (1+4Y) \\ (Y+\cos^2\beta)^2 & = & \cos^2\beta\xi (1+4Y) \end{eqnarray*}$$

despejando finalmente $\xi$, resulta

$$\xi =\frac{(Y +\cos^2\beta)^2}{(1+4Y)\cos^2\beta}$$ (4.33)

Con objeto de visualizar mejor el comportamiento de la región compleja, supongamos las gráficas de las ecuaciones (4.29) y (4.33), con lo que resulta la gráfica IV.V, en donde las líneas llenas nos representan el comportamiento de la ecuación (4.29) que resulta ser una familia de hiperbolas y las líneas punteadas nos representan el comportamiento de (4.33) al comparar esta gráfica con la (IV.IV) vemos que concuerda con la forma de la región compleja, esto es, región II-II.