Ahora analizamos una forma, para encontrar el rango de eigenvalores de
una matriz y una condición mecánica para el modelo empleado.
Supongamos que ![]() es una matriz arbitraria y construyamos el problema
de eigenvalores siguiente en forma matricial, esto es:
es una matriz arbitraria y construyamos el problema
de eigenvalores siguiente en forma matricial, esto es:
![\begin{displaymath}
\left[\begin{array}{cccc} & & & \\ & & & \\ a_{i1} & a_{i2}...
...egin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]
\end{displaymath}](img339.gif)

Pasando al lado derecho el término ![]() resulta:
resulta:
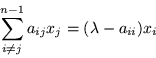
Como siempre existe por lo menos un eigenvector distinto de cero
supongamos que es el ![]() , por lo tanto la ecuación anterior
resulta:
, por lo tanto la ecuación anterior
resulta:
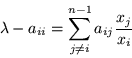
Supongamos además, que la componente ![]() -ésima de este
eigenvector tiene el módulo máximo, llamémosla
-ésima de este
eigenvector tiene el módulo máximo, llamémosla ![]() por lo tanto
resulta, tomando además el valor absoluto en ambos miembros que:
por lo tanto
resulta, tomando además el valor absoluto en ambos miembros que:
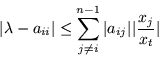
Como ![]() es posible suponer que
es posible suponer que
![]() por lo tanto resulta
finalmente que:
por lo tanto resulta
finalmente que:
Este resultado es conocido como ``teorema de Gerschgorin''
(Ref. [12]) que nos dice: Que en el plano complejo cada eigenvalor de
la matriz de elementos complejos ![]() , se encuentra localizado en al
menos uno de los círculos con centro
, se encuentra localizado en al
menos uno de los círculos con centro ![]() y radio
y radio
![]() (que es la suma de los elementos de un
renglón).
(que es la suma de los elementos de un
renglón).
Como no sabemos cual de las componentes es la máxima, entonces se construyen los discos para cada una de las componentes y si no es el disco que interesa, no lo tomamos en cuenta, pero si lo es, entonces va a incluir el eigenvalor en cuestión; aunque es posible que al cambiar el eigenvalor cambie el elemento donde se alcanza el máximo, pero no importa, ya que se tienen todos los discos y en algunos de ellos se encuentra el eigenvalor.
Por lo tanto lo anterior nos da una información de los
eigenvalores en particular, en el caso que estamos tratando, nos dice
que se tienen un círculo con centro ![]() y radio
y radio ![]() .
Naturalmente que para nuestro problema únicamente nos interesa la
línea real, ya que se trata de una matriz hermitiana con eigenvalores
reales, o sea que el intervalo de eigenvalores para el modelo que
estamos analizando es:
.
Naturalmente que para nuestro problema únicamente nos interesa la
línea real, ya que se trata de una matriz hermitiana con eigenvalores
reales, o sea que el intervalo de eigenvalores para el modelo que
estamos analizando es:
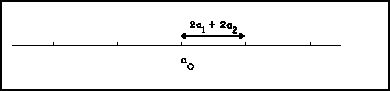
Ahora en el caso de vibraciones mecánicas, se tiene la siguiente
restricción
![]() . Esto quiere decir que la suma de
los elementos a través de un renglón tiene que ser cero. Esta
condición es debida a que un desplazamiento, en una dirección produce
una fuerza la cual produce un desplazamiento en otra dirección y
debido a que el efecto de estas fuerzas es producido por resortes que
se encuentran a ambos lados de las partículas, entonces son los
resortes los que dan lugar a las constantes que intervienen en la
condición mecánica. Esta condición mecánica se puede
visualizar mejor, por medio de un diagrama de fuerzas, esto es
. Esto quiere decir que la suma de
los elementos a través de un renglón tiene que ser cero. Esta
condición es debida a que un desplazamiento, en una dirección produce
una fuerza la cual produce un desplazamiento en otra dirección y
debido a que el efecto de estas fuerzas es producido por resortes que
se encuentran a ambos lados de las partículas, entonces son los
resortes los que dan lugar a las constantes que intervienen en la
condición mecánica. Esta condición mecánica se puede
visualizar mejor, por medio de un diagrama de fuerzas, esto es

Como vemos en este diagrama de fuerzas, si movemos una partícula desde su posición de equilibrio, el efecto de la interacción en ambos lados debe ser el mismo debido a la simetría de la cadena, por lo tanto va a interaccionar con las partículas en ambos lados y es precisamente la constante del resorte la que influye en el equilibrio de fuerzas.
La restricción es gráficamente razonable de postular,
únicamente para nuestro caso que es un sistema vibracional, ya que
en otros sistemas no es válida, como por ejemplo en problemas de
mecánica cuántica, esto es sistema de electrones ![]() .
.
Además si no fuera físicamente razonable postular que
![]() y la empleáramos, el resultado sería
únicamente una traslación de todos los eigenvalores, como lo
podemos ver del siguiente hecho.
y la empleáramos, el resultado sería
únicamente una traslación de todos los eigenvalores, como lo
podemos ver del siguiente hecho.
Tenemos la restricción en la forma:
| (4.4) |
lo cual nos permite escribir esto como
Sustituyendo el valor de ![]() resulta finalmente:
resulta finalmente:
Analizando este resultado, vemos una justificación más de
que las frecuencias resultan imaginarias, con la posibilidad de que
sean cero, pero nunca tendremos el caso ![]() . Otro resultado
que nos da es la justificación del denominador de la relación
(4.2).
. Otro resultado
que nos da es la justificación del denominador de la relación
(4.2).
Por lo tanto de (4.5) y (4.2) resulta:
Al menos en el rango en que ![]() y
y ![]() ya que debido a la
estabilidad de las redes, puede suceder que
ya que debido a la
estabilidad de las redes, puede suceder que ![]() o que
o que ![]() sea
negativa también y puede darse el caso en que estas dos constantes
sean iguales (como se verá al analizar modelos especiales), por lo
tanto es posible obtener interacciones negativas.
sea
negativa también y puede darse el caso en que estas dos constantes
sean iguales (como se verá al analizar modelos especiales), por lo
tanto es posible obtener interacciones negativas.
Ahora lo que nos interesa es calcular los eigenvalores de la
matriz ![]() en términos de los parámetros (2.13), esto es
en términos de los parámetros (2.13), esto es
![]() y
y ![]() por lo tanto seguimos tratando una
cadena homogénea, en este caso la ecuación característica de
por lo tanto seguimos tratando una
cadena homogénea, en este caso la ecuación característica de
![]() , como vimos anteriormente (Ec. 2.21) es
, como vimos anteriormente (Ec. 2.21) es
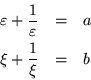
| (4.8) | |||
| (4.9) |
Resolviendo este sistema de ecuaciones resulta:
| (4.10) |
Además estamos interesados en regiones en que ``![]() '' es
complejo o real puro (si es real puro, entonces debe ser mayor o menor
que uno en valor absoluto), así como analizar el efecto de si las
mismas raíces son puramente imaginarias o puramente reales.
'' es
complejo o real puro (si es real puro, entonces debe ser mayor o menor
que uno en valor absoluto), así como analizar el efecto de si las
mismas raíces son puramente imaginarias o puramente reales.
La condición para que sea real puro es que el descriminante de
la ecuación sea cero, esto es:
Que es exactamente la misma relación que se obtiene al considerar únicamente la condición mecánica, después de ciertos artificios matemáticos.
Otro resultado importante que se puede deducir de las ecuaciones anteriores, es la relación entre las constantes de interacción a primeros y segundos vecinos, esto lo podemos ver de la siguiente manera.
Usando el resultado de que
Analizando esta última desigualdad vemos que
Anteriormente mencionamos como una relación de dispersión
puede ser deducida, a partir de la ecuación característica, la
obtención es directa como podemos apreciarlo de la siguiente forma:
Usando la ecuación (4.6), junto con los parámetros
definidos en (2.13) resulta:
| (4.12) |
La gráfica de esta relación de dispersión es la siguiente:
Otra relación de dispersión que nos puede dar bastante información se obtiene de la siguiente forma.
Pongamos los elementos de la matriz de transferencia ![]() y
y
![]() en función de
en función de ![]() y de
y de ![]() , esto es, de (4.1) y
(4.2) resulta:
, esto es, de (4.1) y
(4.2) resulta:
Para solucionar este sistema de ecuaciones, despejamos ![]() de
(4.3) y sustituyámoslo en (4.14) resultando
de
(4.3) y sustituyámoslo en (4.14) resultando
Por lo tanto las soluciones para ``![]() '' están dadas por
'' están dadas por
Esta ecuación es una relación de dispersión porque
relaciona a ``![]() '' como función de
'' como función de ![]() y
y ![]() y de las
constantes del modelo, además se tienen dos alternativas para tratar
esta ecuación; una es solucionar
y de las
constantes del modelo, además se tienen dos alternativas para tratar
esta ecuación; una es solucionar ![]() ó
ó ![]() dependiendo de la conveniencia.
dependiendo de la conveniencia.
Es conveniente poner la ecuación (4.15) en una forma
más explícita anteriormente definimos
Por lo tanto la ecuación (4.15) queda finalmente como:
Que es la relación de dispersión para el interior de cualquier cadena por lo tanto es conveniente analizarla en forma detallada.
Lo que interesa en principio es analizar cuándo la expresión
es real o compleja, ya que si ![]() es complejo necesariamente
que
es complejo necesariamente
que ![]() lo es también.
lo es también.
Por lo tanto la frontera entre real y complejo es cuando el
discriminante de (4.16) es igual a cero, esto es
| (4.17) |
Esta ecuación la podemos graficar, ya que ![]() por lo
tanto es necesario analizarla en la forma siguiente:
por lo
tanto es necesario analizarla en la forma siguiente: ![]() tiene un
polo en
tiene un
polo en ![]() .
.
Cuando
![]() entonces
entonces
![]() y si
y si
![]() entonces
entonces
![]() .
.
Para obtener un extremo calculemos la derivada, esto es
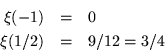
Y es fácil comprobar que ocurre un mínimo en
![]() . También es posible ver cuando la expresión es
positiva o negativa si
. También es posible ver cuando la expresión es
positiva o negativa si
![]() y
y
![]() entonces
entonces ![]() lo cual nos indica que la expresión es negativa.
lo cual nos indica que la expresión es negativa.
Además, cuando ![]() entonces
entonces
Con todos estos datos podemos construir la gráfica de la
frontera entre la parte real y compleja ![]() , gráfica IV-II.
, gráfica IV-II.
Como se puede ver, por combinaciones de ![]() y
y ![]() en la
región compleja
en la
región compleja ![]() es complejo, lo cual quiere decir que
es complejo, lo cual quiere decir que
![]() es complejo, es decir, la frecuencia en esta región vamos a
ver una onda oscilatoria con factor exponencial.
es complejo, es decir, la frecuencia en esta región vamos a
ver una onda oscilatoria con factor exponencial.
Analicemos las diferentes regiones correspondientes a los
distintos valores que puede tomar el parámetro ![]() definido como
definido como
Caso Real.
![]() real
real
Caso Imaginario
![]()
Caso en que existe un cambio de fase.
![]() es real, entonces resulta
es real, entonces resulta
Ahora estamos interesados en contornos en los que ![]() pasa, por
estos puntos, para lo cual es necesario hacer algunas manipulaciones
algebraícas del
pasa, por
estos puntos, para lo cual es necesario hacer algunas manipulaciones
algebraícas del
![]() , en la forma siguiente: De
(4.16) tenemos que:
, en la forma siguiente: De
(4.16) tenemos que:

Que es finalmente la relación de dispersión para el interior
de cualquier cadena, que nos interesa graficar e interpretar
físicamente, además graficaremos ![]() ya que se desean
encontrar contornos con
ya que se desean
encontrar contornos con ![]() fijo.
fijo.
Analizando la ecuación (4.19), vemos que es necesario
tomar valores seleccionados de ![]() para poder interpretar la
gráfica, por lo tanto, si hacemos
para poder interpretar la
gráfica, por lo tanto, si hacemos ![]() , ó
, ó ![]() obtendremos las
fronteras de las curvas que separan las partes real e imaginaria pura,
esto es:
obtendremos las
fronteras de las curvas que separan las partes real e imaginaria pura,
esto es:
Si ![]() entonces:
entonces:
Si ![]() resulta:
resulta:
| (4.20) |
Debido a que
![]() , entonces puede ser que la
, entonces puede ser que la ![]() dada por (4.19) se escape de los límites, por lo tanto es
necesario analizar su comportamiento gráficamente. De (4.19)
resulta:
dada por (4.19) se escape de los límites, por lo tanto es
necesario analizar su comportamiento gráficamente. De (4.19)
resulta:
Si
![]() entonces
entonces
![]()
Si
En
Por lo tanto con estos elementos podemos graficar la ecuación
(4.19) esto es:
Prosiguiendo el análisis de la ecuación (4.18). Si
![]() entonces
entonces
Cuando ![]() , entonces como
, entonces como
![]() necesariamente
necesariamente
![]() , pero cuando
, pero cuando ![]() , las condiciones varían ligeramente.
, las condiciones varían ligeramente.
En
![]() existe una línea crítica ya que
existe una línea crítica ya que
En ![]() la relación entre
la relación entre ![]() y
y ![]() es:
es:
Por lo tanto, como las gráficas (IV.II) y (IV.III) pertenecen a la misma ecuación, deducidas únicamente con análisis diferentes, entonces podemos superponerlas y formar una sola, juntamente con los resultados del análisis de dicha ecuación (4.18), esto es
Analizando esta gráfica, junto con las ecuaciones (4.18) y (2.20) resultan las siguientes regiones características:
Anteriormente vimos que las raíces ocurren en parejas recíprocas por lo tanto en la gráfica IV.IV la interpretación que se le da a cada punto, es que está representando por la intercepción de dos ondas, esto es el movimiento está representado por dos ondas que viajan en direcciones opuestas, entonces vemos el porque en la gráfica (IV.IV) aparecen las superposiciones de dos tipos de ondas.