Comparación entre el modelo cíclico y el de extremos fijos.

Comparemos el modelo cíclico (esto es, el anillo), con el modelo de extremos fijos (que denotamos $M_f$); en este caso tenemos que calcular

$$M_c-M_f = \left[\begin{array}{cccccccc} a_0 & a_1 & a_2 & & & \cdots & a_2 ... ...& & & \ddots & & \\ & & & & a_0 & a_1 \\ & & & & a_1 & a_0 \end{array}\right]$$

$$= \left[\begin{array}{cccccccc} 0 & 0 & 0 & & & \cdots & a_2 & a_1 ... ... a_2 & & & & & & & 0 \\ a_1 & a_2 & & & & & 0 & 0 \end{array}\right] = D_{cf}$$ (10.6)

Como vemos el cálculo de los eigenvalores es inmediato, ya que la parte central de la matriz diferencia $(D_{cf})$ contiene puros ceros, por lo tanto la matriz $4\times 4$ es la que nos interesa; esto es:

$$\left\vert\begin{array}{rrrr} -\mu & 0 & a_2 & a_1 \\ 0... ...begin{array}{rr} a_2 & -\mu \\ a_1 & 0 \end{array}\right\vert$$

Que es simplificado finalmente como

$$(\mu -a_1\mu -a_2^2) (\mu^2 -a_2^2 +a_1\mu) = 0$$

por lo tanto las raíces serán:

$$\begin{eqnarray*} \mu_{1,2} & = & \frac{ a_1\pm \sqrt{a_1^2 +4a_2^2}}{2} \\ \mu_{3,4} & = & \frac{-a_1\pm \sqrt{a_1^2 +4a_2^2}}{2} \end{eqnarray*}$$

Como vemos las raíces ocurren en parejas negativas, ya que $\mu_1 =-\mu_4$ y $\mu_2 =-\mu_3$ como tenía que esperarse de una matriz antisimétrica.

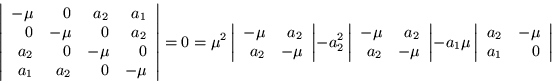
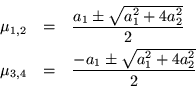
Por lo tanto la transición del modelo cíclico al de extremos fijos no se puede llevar a cabo por adición de una transformación ``definida''. Además la matriz $D_{cf}$ dada por (10.6) tiene traza cero por lo tanto no puede ser definida.