Comparación entre el modelo libre con el de fijos.

Relación de eigenvalores entre el modelo de extremos fijos $(M_f)$ con el de extremos libres $(M_L)$ tenemos que calcular

$$M_L -M_f = \left[\begin{array}{cccccc} a_0^{\prime} & a... ... & & & a_1 \\ & & & & a_1 & a_0 \end{array}\right] =D_{Lf}$$ (10.7)

Por lo tanto la matriz diferencia toma la forma

$$D_{Lf} =\left[\begin{array}{cccc} a_1 +a_2 & 0 & 0 & 0 \\ ... ... 0 & 0 & a_2 & 0 \\ 0 & 0 & 0 & a_1 +a_2 \end{array}\right]$$

Calculando los eigenvalores, para ver que tipo de matriz es

$$\left\vert\begin{array}{cccc} a_1 +a_2 -\mu & 0 & 0 & 0 \\... ... & 0 \\ 0 & 0 & 0 & a_1 +a_2 -\mu \end{array}\right\vert = 0$$

Por lo consiguiente:

$$(a_1 +a_2 -\mu)^2 (a_2 -\mu)^2 = 0$$

Con lo cual las raíces son

$$\begin{eqnarray*} \mu_{1,2} & = & a_1 +a_2 \\ \mu_{3,4} & = & a_2 \end{eqnarray*}$$

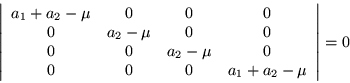
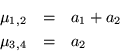
Por lo tanto podemos concluir que la matriz $D_{Lf}$ es positiva definida, esto es cumple que

$$(x, D_{Lf} x) \geq 0$$

Ahora de la relación dada por (10.7) resulta

$$M_L =M_f +D_{Lf}$$ (10.8)

Aplicando el producto interior a ambos lados de esta igualdad tenemos que:

$$(x,M_L x) =(x, (M_f +D_{Lf})x)$$

Debido a la linealidad del producto interior, resulta que

$$(x, M_L x) =(x,D_{Lf}x) +(x, M_f x)$$

Aplicando el resultado, de que la matriz $D_{Lf}$ es positiva definida.

$$(x, M_L x) \geq (x, M_f x)$$

resulta finalmente

$$M_L \geq M_f$$ (10.9)

O sea podemos concluir, que cuando ordenamos los eigenvalores en parejas, los eigenvalores del modelo libre siempre son mayores que los del modelo de los extremos fijos.

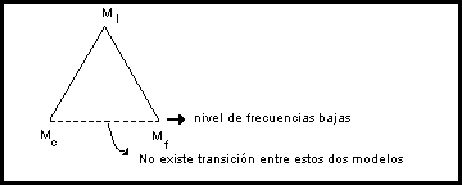
Por lo tanto de acuerdo con el rango de eigenvalores, podemos representar los resultados de estos tres modelos en la forma siguiente.