Anteriormente vimos un teorema, el cual nos permite obtener un disco, cuyo centro es el valor del elemento diagonal principal y radio la suma de los valores absolutos de los demás elementos que están sobre un renglón fuera de la diagonal principal, así se tienen discos, en los cuales existe la posibilidad de tener el eigenvalor en el interior de alguno de ellos.
Lo importante del resultado que se obtiene, cuando la suma de
los elementos de un renglón es cero, es no sólo que nos permite
encontrar que ![]() es un eigenvalor, sino además que los
elementos en la diagonal principal son negativos, por lo cual si
consideramos un plano sobre el cual se encuentre el disco, tendremos
que en este caso, se encontrará en el lado izquierdo, entonces se
pueden tener varios discos, si los renglones son distintos, pero todos
quedarán en la mitad izquierda del plano, esto es.
es un eigenvalor, sino además que los
elementos en la diagonal principal son negativos, por lo cual si
consideramos un plano sobre el cual se encuentre el disco, tendremos
que en este caso, se encontrará en el lado izquierdo, entonces se
pueden tener varios discos, si los renglones son distintos, pero todos
quedarán en la mitad izquierda del plano, esto es.
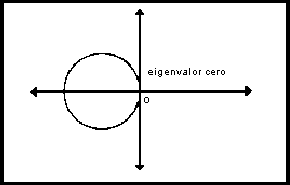
Por lo tanto se tiene que cero es un eigenvalor y que todos los
demás están a la izquierda del plano y en el interior del disco,
como se puede apreciar del diagrama; entonces sabemos que todos los
![]() 's son negativos, por lo tanto se tiene que la matriz es
negativa semidefinida, la cual es una condición necesaria y
suficiente, que está en concordancia con el álgebra matricial, ya
que se dice que una matriz simétrica es negativa semidefinida, si y
solo si todos sus eigenvalores son negativos.
's son negativos, por lo tanto se tiene que la matriz es
negativa semidefinida, la cual es una condición necesaria y
suficiente, que está en concordancia con el álgebra matricial, ya
que se dice que una matriz simétrica es negativa semidefinida, si y
solo si todos sus eigenvalores son negativos.
Por lo tanto la posición del disco depende de los signos relativos, del elemento de la diagonal principal y de los que están fuera de la diagonal principal; también los cambios en los signos relativos dan lugar a los cambios en los eigenvalores.
Por otra parte la estabilidad de una red (ver Ref. [6]),
se supone que es asociada con una forma cuadrática positiva definida
para la energía de tensión. En el caso de un continuo
unidimensional que es el que estamos analizando, la condición de
estabilidad degenera al requisito simple de un módulo de Young
positivo, el cual puede expresarse como función de las constantes de
fuerza ![]() y
y ![]() ' o bien por los elementos matriciales
' o bien por los elementos matriciales ![]() y
y
![]() ; esto es llevado a cabo por expander los desplazamientos en
series de Taylor y retener términos cuadráticos comparados con la
distancia interatómica.
; esto es llevado a cabo por expander los desplazamientos en
series de Taylor y retener términos cuadráticos comparados con la
distancia interatómica.
En nuestro modelo, se puede demostrar que el módulo de Young
depende de los signos relativos de ![]() , esto es, en el caso de que
, esto es, en el caso de que
![]() se dice que la red es estable. Cuando
se dice que la red es estable. Cuando ![]() se tiene un
equilibrio crítico, ya que este en este caso las fuerzas
atractivas y repulsivas casi serán iguales (esto pasa en la
frontera). En el caso de que
se tiene un
equilibrio crítico, ya que este en este caso las fuerzas
atractivas y repulsivas casi serán iguales (esto pasa en la
frontera). En el caso de que ![]() existe mayor atracción con lo
cual hay mayor estabilidad, entonces
existe mayor atracción con lo
cual hay mayor estabilidad, entonces ![]() tiene que ser negativo,
esto puede deducirse de condiciones físicas, en el sentido de la
clase de equilibrio que se tenga, es decir, elástico o estático.
tiene que ser negativo,
esto puede deducirse de condiciones físicas, en el sentido de la
clase de equilibrio que se tenga, es decir, elástico o estático.
Por lo tanto lo anterior depende del hecho de que, los elementos
de un renglón sumados o restados nos hagan cero el renglón, esto
no se puede asegurar completamente en todos los modelos, pero lo que
sí se puede asegurar es que todos los eigenvalores van a subir o
bajar, particularmente se puede aplicar al caso cuando la frontera es
suave o dura, se puede pensar que debido a la falta de átomos de un
lado de la cadena o de un sólido en general, las fuerzas de
atracción son más grandes (esto es conocido por resultados
experientales), ya que si las fuerzas repulsivas fueran las mayores,
tendríamos una frontera difusa, podemos suponer que en la frontera
la superficie es más densa lo cual quiere decir que
![]() y que
y que
![]() ; por lo tanto va a ser
necesario modificar la matriz por el cambio de estos tres elementos, e
igualmente si se desea hacer el cambio en la frontera opuesta;
entonces vamos a considerar una cadena con interacciones, en la forma
siguiente
; por lo tanto va a ser
necesario modificar la matriz por el cambio de estos tres elementos, e
igualmente si se desea hacer el cambio en la frontera opuesta;
entonces vamos a considerar una cadena con interacciones, en la forma
siguiente
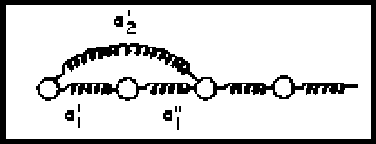
Por lo tanto tendremos una submatriz ![]() en cada una de las
esquinas, representando la perturbación en sus extremos respectivos.
Con objeto de simplificar el álgebra únicamente consideraremos la
perturbación en un extremo, esto es.
en cada una de las
esquinas, representando la perturbación en sus extremos respectivos.
Con objeto de simplificar el álgebra únicamente consideraremos la
perturbación en un extremo, esto es.
La matriz sin perturbar
![\begin{displaymath}
M=\left[\begin{array}{ccccccc}
a_0 & a_1 & a_2 & & & & \\...
...1 & a_2 & \\
\vdots & & & & & & \ddots
\end{array}\right]
\end{displaymath}](img969.gif)
Por lo tanto la submatriz con la perturbación tiene la forma
![\begin{displaymath}
M' =\left[\begin{array}{ccc}
-a_1^{\prime}-a_2^{\prime} &...
...} & -a_2^{\prime} -a_1^{\prime\prime} \\
\end{array}\right]
\end{displaymath}](img970.gif)
Para obtener la ecuación característica y por lo tanto
los eigenvalores hagamos:
![]() y
y
![]() ;
con lo que la ecuación característica toma la forma
;
con lo que la ecuación característica toma la forma
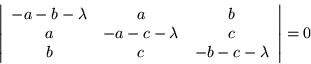
Ahora lo que nos interesa, es ver si estos eigenvalores
![]() son negativos, para esto calculemos
explícitamente
son negativos, para esto calculemos
explícitamente
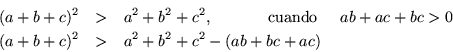
Analizando este resultado, junto con (10.10) vemos que los
eigenvalores ![]() son negativos, lo cual quiere decir que
la matriz
son negativos, lo cual quiere decir que
la matriz ![]() para este caso es negativa semidefinida. Por lo tanto
tal situación siempre tiene que ocurrir, cuando la suma-renglón es
cero y los elementos son positivos.
para este caso es negativa semidefinida. Por lo tanto
tal situación siempre tiene que ocurrir, cuando la suma-renglón es
cero y los elementos son positivos.
Supongamos que hacemos los resortes extremos más fuertes al sumar esta matriz negativa semidefinida, entonces lo que va a ocurrir es que únicamente podemos bajar los eigenvalores, (elevándose las frecuencias) como es apropiado a resortes duros, esto es, a superficies duras. Recíprocamente, una superficie suave bajará las frecuencias, lo que corresponde a que los eigenvalores (negativos) crezcan.
También notamos que la misma consideración se aplica a la
interacción de primeros y segundos vecinos; si ![]() es positivo
todas las frecuencias crecerán.
es positivo
todas las frecuencias crecerán.
Prosiguiendo con esta idea, que pasará si ![]() es medida
en unidades de
es medida
en unidades de ![]() y
y ![]() se incrementa, entonces
se incrementa, entonces
![]() puede o no crecer, o puede anularse, tal
consideración no se aplica al interior de la cadena en donde
puede o no crecer, o puede anularse, tal
consideración no se aplica al interior de la cadena en donde ![]() y
y
![]() peramencen constantes, cuando las
peramencen constantes, cuando las ![]() 's extremas se modifican.
's extremas se modifican.
Por lo tanto hasta cierto límite se puede aplicar el teorema de comparación de eigenvalores.
Así cuando se hacen cambios en las dos esquinas opuestas a la diagonal, pero sin modificar los términos del interior, lo cual da lugar a que el disco quede centrado en el origen, (en lugar de estar situado en el semiplano negativo) lo que implicará que algunos eigenvalores resulten positivos y otros negativos, entonces las frecuencias en un caso van a bajar y en el otro van a subir, pero en partes distintas del espectro; como vemos va a existir una gran cantidad de consideraciones, así que el cambio de un elemento de la matriz, nos da la posibilidad de un aumento de algunos eigenvalores y la disminución de otros, dependiendo del grado de la perturbación; si ajustamos el elemento diagonal, al mismo tiempo, podemos darnos cuenta que todos los eigenvalores van en la misma dirección, lo cual es razonable, ya que sumar a la diagonal, equivale a sumar algo a los eigenvalores.
Siguiendo con esta idea, veamos que pasa si cambiamos los elementos de
la frontera de la diagonal principal, esto es
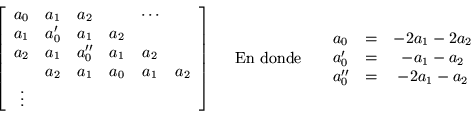
![\begin{displaymath}
\left[\begin{array}{ccc}
a_0^{\prime} & a_1 & a_2 \\
a_...
..._2 \\
a_1 & -a_1 & 0 \\
a_2 & 0 & -a_2 \end{array}\right]
\end{displaymath}](img985.gif)
Calculando la ecuación característica, con objeto de
determinar el tipo de matriz, resulta:
![\begin{displaymath}
\left\vert\begin{array}{ccc}
-a_1-a_2-\xi & a_1 & a_2 \\ ...
...\end{array}\right]
=\xi (\xi^2 +2\xi(a_1+a_2) +3a_1a_2) = 0
\end{displaymath}](img986.gif)
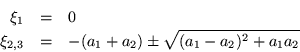
Por un álgebra similar a la anterior resulta que
![\begin{displaymath}
\left[\begin{array}{cc}
0 & \\
& \mbox{Cadena libre} \\ ...
...
\mbox{part\'{\i}culas} \\
\\
\\ \end{array}\right]\;\;\;
\end{displaymath}](img989.gif)
Desde luego que la matriz suma es negativa, además cada
frecuencia de la cadena con ![]() partículas es mayor que la
correspondiente frecuencia de la cadena con
partículas es mayor que la
correspondiente frecuencia de la cadena con ![]() partículas,
resultado análogo al teorema de alternación de eigenvalores
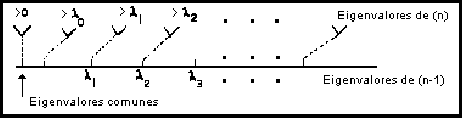
(Ref. [15]), gráficamente tendremos
partículas,
resultado análogo al teorema de alternación de eigenvalores
(Ref. [15]), gráficamente tendremos

Si empleamos el teorema de alternación de eigenvalores para una submatriz, tendremos
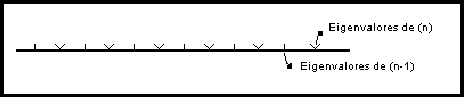
Sin embargo, el teorema sólo no nos permite simultáneamente modificar los elementos matriciales diagonales, así que la matriz negativa semidefinida es necesaria después de todo. Sin embargo, eso nos da una desigualdad, pero no confina el intervalo (podríamos obtener el mismo teorema, aún con una enorme perturbación, así que allí puede no existir confinamiento).
Por lo tanto el teorema en forma gráfica tiene la forma