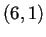
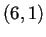
El autómata ![]() a tomar será el resultado del producto cartesiano de un autómata
a tomar será el resultado del producto cartesiano de un autómata ![]() y un autómata
y un autómata ![]() . El primero usa la regla
. El primero usa la regla ![]() la cual sabemos es un corrimiento a la izquierda y tiene índices de Welch
la cual sabemos es un corrimiento a la izquierda y tiene índices de Welch ![]() y
y ![]() . El segundo un autómata
. El segundo un autómata ![]() usa la regla
usa la regla ![]() que es un corrimiento a la derecha con índices de Welch
que es un corrimiento a la derecha con índices de Welch ![]() y
y ![]() . Con estos dos autómatas obtenemos un autómata
. Con estos dos autómatas obtenemos un autómata ![]() con regla ZWEZWEZWEZWEZWEZWESP7SP7SP7SP7SP7SP7LI0LI0LI0LI0LI0
LI0ZWEZWEZWEZWEZWEZWESP7SP7SP7SP7SP7SP7LI0LI0LI0LI0LI0LI0, la cual tiene índices de Welch
con regla ZWEZWEZWEZWEZWEZWESP7SP7SP7SP7SP7SP7LI0LI0LI0LI0LI0
LI0ZWEZWEZWEZWEZWEZWESP7SP7SP7SP7SP7SP7LI0LI0LI0LI0LI0LI0, la cual tiene índices de Welch ![]() y
y ![]() .
.
Como podemos observar en la Figura 4.22, el comportamiento de este autómata reversible ![]() es de un corrimiento cruzado, conservando las características de la evolución de los autómatas
es de un corrimiento cruzado, conservando las características de la evolución de los autómatas ![]() y
y ![]() de los cuales se originó.
de los cuales se originó.
Debido a que el autómata tiene ![]() nodos en su diagrama de de Bruijn, su diagrama de parejas y de subconjuntos resultan demasiado extensos para graficar.
nodos en su diagrama de de Bruijn, su diagrama de parejas y de subconjuntos resultan demasiado extensos para graficar.
Dado que en este autómata existen tantas secuencias de tamaño ![]() como
como ![]() , resulta muy extenso enumerar todas las permutaciones de estas cadenas como se ha venido haciendo con los ejemplos anteriores, sin embargo, se enumeraran unas cuentas para ejemplificar el proceso. Generemos una secuencia inicial de
, resulta muy extenso enumerar todas las permutaciones de estas cadenas como se ha venido haciendo con los ejemplos anteriores, sin embargo, se enumeraran unas cuentas para ejemplificar el proceso. Generemos una secuencia inicial de ![]() células y hagamos tres evouciones de las mismas.
células y hagamos tres evouciones de las mismas.
Tomemos las secuencias que aparecen en la evolución, utilizando el proceso descrito en la sección 4.3 formemos las permutaciones ![]() y
y ![]() para estas cadenas, como se hizo con los ejemplos anteriores.
para estas cadenas, como se hizo con los ejemplos anteriores.
|
Con estas permutaciones, tratemos de reproducir la evolución del autómata empezando desde la misma secuencia inicial.
El proceso funciona de la manera esperada; con estos ejemplos hemos podido visualizar que el ajuste hecho al método de Kari nos brinda una manera de representar la evolución de un autómata reversible por medio de dos permutaciones en bloque y un corrimiento, sin importar el valor que tengan los índices de Welch ni que su tamaño de vecindad sea par o impar.