




Siguiente: Subvariedad
abierta de una
Arriba: Variedades
con borde
Anterior: Variedades
con borde
Como antes (como en la sección 5.4.2, por mencionar sólo un
caso),  designamos por
designamos por 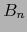 la bola euclidiana patrón,
abierta, en
la bola euclidiana patrón,
abierta, en 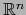 :
:
donde  es la norma euclidiana, y por
es la norma euclidiana, y por
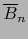 su
adherencia, vale decir, la correspondiente bola cerrada:
su
adherencia, vale decir, la correspondiente bola cerrada:
Definimos la aplicación
![$\varphi \colon ]-1,0] \times S^n \to {\overline
B}_{n+1} - \{ 0 \}$](img4907.png) por:
por:
 es una biyección y
es una biyección y
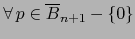 vale:
vale:
Notamos que la aplicación
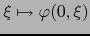 es la
identidad de
es la
identidad de  .
.  es la
restricción a
es la
restricción a ![$]-1,0]\times S^n$](img29.png) de la aplicación continua
de la aplicación continua
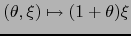 de
de
 en
en
 , luego
, luego  es
continua. A su vez,
es
continua. A su vez, 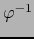 es la
restricción a
es la
restricción a 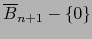 de la aplicación continua
de la aplicación continua
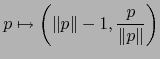 de
de
 en
en
 , luego
también
, luego
también 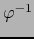 es continua.
Así pues,:
es continua.
Así pues,:
 es un homeomorfismo de
es un homeomorfismo de
![$]-1,0]\times S^n$](img29.png) sobre
sobre
 .
.
Como en la sección 5.4.2
consideramos ![$\forall \, i \in [\![ 1, n+1 ]\!]$](img4431.png) y para
y para
 los conjuntos (hemisferios
abiertos):
los conjuntos (hemisferios
abiertos):
y recordamos que la familia
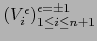 es un recubrimiento
abierto de
es un recubrimiento
abierto de  .
.
![$\forall \, i \in [\![ 1, n+1 ]\!]$](img4431.png) y
y
 ponemos:
ponemos:
Por ser  un homeomorfismo, la familia
un homeomorfismo, la familia
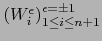 es un
recubrimiento abierto
del espacio
es un
recubrimiento abierto
del espacio 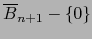 .
.
Designamos por 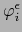 la restricción de la aplicación
la restricción de la aplicación
 al conjunto
al conjunto
![$]-1,0] \times V_i^\epsilon$](img4922.png) .
.
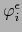 es un homeomorfismo del conjunto
es un homeomorfismo del conjunto
![$]-1,0] \times V_i^\epsilon$](img4922.png) sobre el abierto
sobre el abierto  de
de
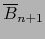 .
.
Designamos por 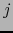 la identidad del intervalo
la identidad del intervalo ![$]-1,0]$](img4926.png) y volvemos a los
mapas
y volvemos a los
mapas 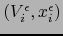 de
de  de la
sección 5.4.2.
Recordamos que
de la
sección 5.4.2.
Recordamos que 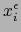 es el homeomorfismo
de
es el homeomorfismo
de 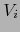 sobre
sobre 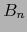 dado por:
dado por:
Introduzcamos ahora ![$\forall \, i \in [\![ 1, n+1 ]\!]$](img4431.png) y
y
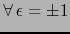 , la
aplicación
, la
aplicación
![$y_i^\epsilon \colon W_i^\epsilon \to
]-1,0] \times B_n$](img4930.png) que definimos por:
que definimos por:
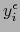 es un homeomorfismo del abierto
es un homeomorfismo del abierto  de
de
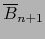 sobre el abierto (de
sobre el abierto (de
segunda especie) del
semiespacio cerrado 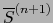 de
de
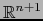 , o sea, los
, o sea, los
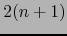 pares
pares
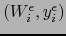
![$i \in [\![ 1,n+1 ]\!]$](img4447.png) ,
,
 son mapas de
son mapas de 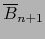 (de segunda
especie) en el semiespacio cerrado
(de segunda
especie) en el semiespacio cerrado
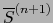 de
de
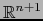 . Véase la figura 5.2.
. Véase la figura 5.2.
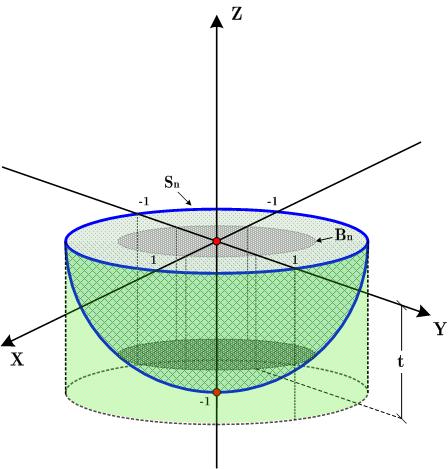
Figure 5.2:
Bosquejo de los homeomorfismos 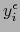 :
el cilindro es
:
el cilindro es ![$]-1,0]\times S^n$](img29.png) y cada plano
y cada plano 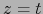 (aquí
(aquí 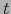 es el parámetro
es el parámetro  en
el texto) corta al cilindro y al hemisferio. El corte en el hemisferio
se proyecta como una esfera en la bola
en
el texto) corta al cilindro y al hemisferio. El corte en el hemisferio
se proyecta como una esfera en la bola 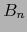 .
.
|
|
Para completar este conjunto de mapas a un atlas de
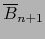 en
en 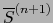 debemos adjuntar un mapa
en el punto cero.
debemos adjuntar un mapa
en el punto cero.
Sea 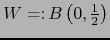 (bola abierta de
centro 0,
de radio
(bola abierta de
centro 0,
de radio 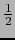 . Si
. Si 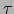 es la
translación de vector
es la
translación de vector
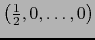 ,
, 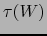 es una bola
abierta de radio
es una bola
abierta de radio 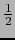 contenida en
contenida en 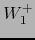 .
Definimos
.
Definimos 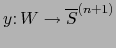 por:
por:
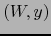 es un mapa de primera especie de
es un mapa de primera especie de
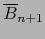 en el
punto
en el
punto 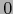 . La familia
. La familia
![$\left( W_i^\epsilon, y_i^\epsilon \right)_{i \in
[\![ 1,n]\!]}^{\epsilon = \pm 1}$](img4943.png) , junto con el mapa
, junto con el mapa 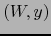 es un atlas
de
es un atlas
de 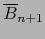 en
en 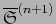 .
Estudiaremos los correspondientes cambios de mapas.
.
Estudiaremos los correspondientes cambios de mapas.
- Empecemos con los cambios de mapas:
Se tiene
![$y_i^\epsilon (W_i^\epsilon \cap
W_k^\eta)\ =\ ]-1,0] \times x_i^\epsilon (V_i^\epsilon \cap V_k^\eta)
\ \subset\ ]-1,0] \times B_n$](img4946.png) .
.
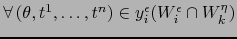 vale:
vale:
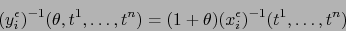 |
(6) |
de donde:
 |
(7) |
Ahora bien, por lo visto en la sección 5.4.2, la aplicación:
es de clase  . Por lo tanto, la
aplicación:
. Por lo tanto, la
aplicación:
del abierto
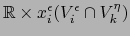 de
de
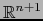 en
en
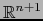 es de clase
es de clase  .
La
fórmula (7) dice que
.
La
fórmula (7) dice que
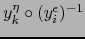 es la
restricción de esta última al abierto
es la
restricción de esta última al abierto
![$]-1,0] \times x_i^\epsilon
(V_i^\epsilon \cap V_k^\eta)$](img4954.png) de segunda especie
de
de segunda especie
de 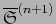 .
.
Así pues, la aplicación
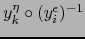 es de clase
es de clase  según la definición 4.6.6.
según la definición 4.6.6.
- Consideremos los cambios de mapas
Usando la fórmula (6) obtenemos:
Luego:
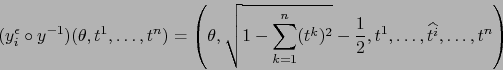 |
(8) |
La fórmula (7)
muestra que el cambio de mapas
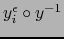 es, en efecto, de
clase
es, en efecto, de
clase  .
.
- Finalmente, consideremos un cambio de mapas:
Por la fórmula (6):
Luego
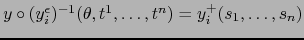 donde
donde
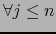 :
:
o sea,:
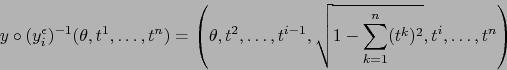 |
(9) |
La fórmula (9)
muestra que el cambio de mapas
 es, en efecto, de
clase
es, en efecto, de
clase  .
.
De los incisos a), b), y c) se desprende
que el atlas que
construimos sobre 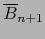 es coherente
es coherente  .
Define sobre
.
Define sobre 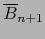 la estructura de una variedad con
borde de clase
la estructura de una variedad con
borde de clase  , de dimensión
, de dimensión 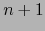 . La llamaremos
ESTRUCTURA NATURAL DE VARIEDAD CON BORDE
sobre
. La llamaremos
ESTRUCTURA NATURAL DE VARIEDAD CON BORDE
sobre 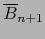 .
.
Sea 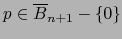 .
.  pertenece a un conjunto
pertenece a un conjunto
 y se tiene:
y se tiene:
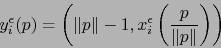 |
(10) |
 pertenece al borde de
pertenece al borde de
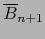 si y sólo si la
primera coordenada de
si y sólo si la
primera coordenada de 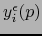 vale cero, o sea,
vale cero, o sea, 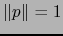 , es
decir
, es
decir  . Así pues:
. Así pues:
Se ve por la fórmula (10) que el mapa
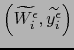 de
de
 inducido por el mapa
inducido por el mapa
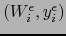 de segunda especie
de
de segunda especie
de 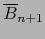 no es otro que
no es otro que
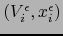 .
Así pues,:
.
Así pues,:
La estructura de variedad  inducida sobre la esfera
inducida sobre la esfera  considerada como borde de
considerada como borde de 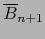 coincide con la
estructura natural de variedad
coincide con la
estructura natural de variedad  de
de  , definida en la sección 5.4.2.
, definida en la sección 5.4.2.





Siguiente: Subvariedad
abierta de una
Arriba: Variedades
con borde
Anterior: Variedades
con borde
Guillermo M. Luna
2009-06-14
![]() designamos por
designamos por ![]() la bola euclidiana patrón,
abierta, en
la bola euclidiana patrón,
abierta, en ![]() :
:
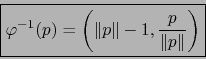
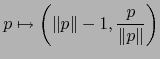 de
de
![]() y para
y para
![]() los conjuntos (hemisferios
abiertos):
los conjuntos (hemisferios
abiertos):
![]() la restricción de la aplicación
la restricción de la aplicación
![]() al conjunto
al conjunto ![]() .
.
![]() es un homeomorfismo del conjunto
es un homeomorfismo del conjunto
![]() sobre el abierto
sobre el abierto ![]() de
de
![]() .
.
![]() la identidad del intervalo
la identidad del intervalo ![]() y volvemos a los
mapas
y volvemos a los
mapas ![]() de
de ![]() de la
sección 5.4.2.
Recordamos que
de la
sección 5.4.2.
Recordamos que ![]() es el homeomorfismo
de
es el homeomorfismo
de ![]() sobre
sobre ![]() dado por:
dado por:
![]() en
en ![]() debemos adjuntar un mapa
en el punto cero.
debemos adjuntar un mapa
en el punto cero. ![]() (bola abierta de
centro 0,
de radio
(bola abierta de
centro 0,
de radio ![]() . Si
. Si ![]() es la
translación de vector
es la
translación de vector
![]() ,
, ![]() es una bola
abierta de radio
es una bola
abierta de radio ![]() contenida en
contenida en ![]() .
Definimos
.
Definimos ![]() por:
por:
![]() vale:
vale: ![]() es de clase
es de clase ![]() según la definición 4.6.6.
según la definición 4.6.6. 
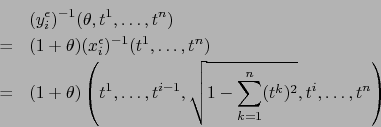
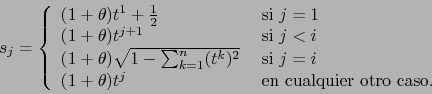
![]() .
. ![]() pertenece a un conjunto
pertenece a un conjunto
![]() y se tiene:
y se tiene:
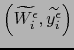 de
de
inducida sobre la esfera
considerada como borde de
coincide con la estructura natural de variedad
de
, definida en la sección 5.4.2.