Un disco euclidiano abierto en
![]() posee, como todo abierto en
posee, como todo abierto en
![]() , una estructura natural de variedad diferenciable: aquélla de
una subvariedad abierta de
, una estructura natural de variedad diferenciable: aquélla de
una subvariedad abierta de
![]() . No así el disco cerrado
correspondiente.
. No así el disco cerrado
correspondiente.
En esta sección veremos cómo, mediante una leve generalización del concepto de variedad diferenciable, espacios como el disco cerrado, un toro sólido junto con la superficie que lo limita y análogos llegan a integrarse a los objetos de nuestro estudio.
Sea
![]() . Designamos por
. Designamos por
![]() (más
frecuentemente sobreentendido
(más
frecuentemente sobreentendido ![]() , simplemente por
, simplemente por
![]() ) el
semiespacio cerrado de
) el
semiespacio cerrado de
![]() :
:
Todo atlas en la clase de equivalencia considerada se dice un ATLAS ADMISIBLE de la variedad con borde.
Un mapa de ![]() se dice MAPA ADMISIBLE DE LA VARIEDAD CON BORDE si es
compatible
se dice MAPA ADMISIBLE DE LA VARIEDAD CON BORDE si es
compatible ![]() con todo mapa de un atlas admisible de dicha variedad
con borde.
con todo mapa de un atlas admisible de dicha variedad
con borde.
Sobreentendiendo (si no hay más que una en consideración) la clase
de equivalencia, se dice por abuso del lenguaje ``![]() es una variedad
es una variedad
![]() ''.
''.
Análogamente al teorema 5.1.8 se prueba:
Un mapa de ![]() es admisible para la variedad con borde si y sólo si es
un mapa de dicho atlas maximal. Un atlas de
es admisible para la variedad con borde si y sólo si es
un mapa de dicho atlas maximal. Un atlas de ![]() en
en
![]() es
admisible para la variedad con borde si y sólo si está contenido en
dicho atlas maximal.
es
admisible para la variedad con borde si y sólo si está contenido en
dicho atlas maximal.
Demostración
A. Afirmamos primero que si ![]() es un mapa admisible de
es un mapa admisible de
![]() , si
, si ![]() es un abierto de
es un abierto de ![]() contenido en
contenido en ![]() y
y ![]() es la
restricción de
es la
restricción de ![]() a
a ![]() , también
, también
![]() es un
mapa admisible de
es un
mapa admisible de ![]() .
.
Debemos probar que el mapa
![]() es compatible
es compatible ![]() con cualquier mapa admisible
con cualquier mapa admisible ![]() de
de ![]() . Ahora bien, el cambio de
mapa:
. Ahora bien, el cambio de
mapa:
B. Sea ![]() tal que para cierto mapa admisible
tal que para cierto mapa admisible ![]() de
de
![]() en
en ![]() se tiene
se tiene
![]() . Sea
. Sea ![]() el
semiespacio abierto de
el
semiespacio abierto de
![]() que corresponde a
que corresponde a
![]() . Vale
. Vale
![]() y, ya que
y, ya que ![]() es abierto en
es abierto en
![]() , se sigue de ahí que
, se sigue de ahí que ![]() es abierto en
es abierto en
![]() , luego en
, luego en
![]() . Se sigue ahora del inciso A) que si
. Se sigue ahora del inciso A) que si
![]() es la restricción de
es la restricción de ![]() a
a
![]() ,
,
![]() es un mapa admisible de primera
especie en
es un mapa admisible de primera
especie en ![]() .
.
![]()
Si para
cierto mapa admisible
![]() en
en ![]() vale
vale
![]() (es decir
(es decir ![]() ), entonces valdrá también para
todo mapa admisible
), entonces valdrá también para
todo mapa admisible
![]() en
en ![]() ,
,
![]() (es decir
(es decir ![]() ).
).
Demostración
Razonando por contradicción supongamos que fuese
![]() e
e
![]() .
.
Por el lema 5.5.1 se puede substituir el mapa ![]() por un mapa
admi-simisible
por un mapa
admi-simisible ![]() de primera especie en
de primera especie en ![]() .
.
El cambio de mapa
![]() sería un isomorfismo
sería un isomorfismo ![]() . Pero
. Pero ![]() es un abierto de
primera especie en
es un abierto de
primera especie en
![]() , pues, lo es
, pues, lo es ![]() , mientras que
, mientras que
![]() es un abierto de segunda especie en
es un abierto de segunda especie en
![]() pues
pues
![]() y
y
![]() . Obtuvimos, pues, una contradicción
con el teorema 4.71 y ésta termina la demostración.
. Obtuvimos, pues, una contradicción
con el teorema 4.71 y ésta termina la demostración.
![]()
Nota 1
Si
![]() ,
, ![]() es simplemente una variedad
diferenciable según las definiciones de la sección 5.1.
es simplemente una variedad
diferenciable según las definiciones de la sección 5.1.
En efecto, una variedad
diferenciable arbitraria de dimensión ![]() , podemos usar solamente
mapas admisible
, podemos usar solamente
mapas admisible ![]() con
con ![]() en el semiespacio abierto
en el semiespacio abierto
![]() .
.
Así pues, una ``variedad diferenciable'' es un caso particular de una ``variedad diferenciable con borde'', pero no al revés.
Esta terminología, contraria a las buenas costumbres matemáticas, está sancionada por la tradición y nolens volens nos hemos plegado a ella.
Nota 2
La mayoría de los autores usa la notación ![]() por el
borde de
por el
borde de ![]() . Ésta constituye en nuestra opinión un empréstito algo
ilegítimo a la topología algebraica, pues, en ésta
. Ésta constituye en nuestra opinión un empréstito algo
ilegítimo a la topología algebraica, pues, en ésta ![]() designa un operador de carácter algebraico.
designa un operador de carácter algebraico.
Demostración
Por el lema 5.5.1
![]() existe un
mapa admisible
existe un
mapa admisible ![]() de
de ![]() en
en ![]() de primera especie, es decir,
de primera especie, es decir,
![]() .
.
El conjunto de todos tales mapas constituye un atlas coherente ![]() maximal de
maximal de
![]() en el sentido de la sección 5.1. Define la
estructura anunciada.
en el sentido de la sección 5.1. Define la
estructura anunciada.
![]()
Demostración
Por el lema 5.5.1,
![]() existe un
mapa
existe un
mapa ![]() de
de ![]() de primera especie en el punto
de primera especie en el punto ![]() .
. ![]() es una
vecindad de
es una
vecindad de ![]() en
en ![]() contenida en
contenida en
![]() . Así pues,
. Así pues,
![]() es una vecindad de cualquiera de sus puntos, por lo
tanto, un conjunto abierto en
es una vecindad de cualquiera de sus puntos, por lo
tanto, un conjunto abierto en ![]() . Luego el conjunto
. Luego el conjunto ![]() es
cerrado en
es
cerrado en ![]() .
.
![]()
Demostración
Escribimos
![]() y designamos por
y designamos por
![]() ,
,
![]() las proyecciones
canónicas, vale decir:
las proyecciones
canónicas, vale decir:
![]()
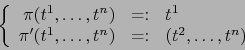
Sea ![]() un mapa admisible de
un mapa admisible de ![]() de segunda especie. Definamos:
de segunda especie. Definamos:
como anunciamos. Notemos la siguiente fórmula de inversión dees un homeomorfismo del abierto
de
sobre el abierto
de
,
Ya que
![]() es de clase
es de clase ![]() ,
la aplicación
,
la aplicación
![]() es de
clase
es de
clase ![]() .
Definimos el conjunto:
.
Definimos el conjunto:
Por la fórmula (4) vale
![]() :
:
Según la fórmula (5), la aplicación
![]() es la restricción al abierto
es la restricción al abierto
![]() de
de
![]() de la aplicación
de la aplicación
![]() definida en el abierto
definida en el abierto
![]() de
de
![]() . De lo dicho arriba se sigue que
. De lo dicho arriba se sigue que
![]() es de clase
es de clase ![]() en
en
![]() . Luego el cambio de mapa
. Luego el cambio de mapa
![]() es de clase
es de clase ![]() en
en
![]() . Así viene probado que los mapas
. Así viene probado que los mapas
![]() y
y
![]() de
de
![]() son compatibles
son compatibles ![]() .
De esto se sigue:
.
De esto se sigue:
Si el mapaEste atlas define sobrerecorre el conjunto de todos los mapas admisibles de segunda especie de la variedad con borde
, el correspondiente mapa
de
recorre un atlas coherente
del espacio
en el sentido de la definición 5.15.