Siguiente: Isomorfismos Arriba: Cálculo diferencial en un Anterior: La funcional

Aplicaciones de clase $C^k$

Definición 6.6   Sean $V$ un abierto de $\overline{ \mbox{\frakiii S}}$ y $\varphi \colon V \to {\cal F}$. Se dice que $\varphi$ es una APLICACIÓN DE CLASE $C^k$ ( $k \in {\mathbb{N}}\cup \{ \infty \}$) en $V$ si existe un abierto $U$ de $\cal E$ tal que $V = U \cap \overline{\mbox{\frakiii S}}$ y una ampliación $\tilde \varphi$ de $\varphi$ a $U$ tal que $\tilde \varphi$ es de clase $C^k$ en $U$ según la definición 4.5.2

Observación 1

Si V es un abierto de primera especie en $\overline{ \mbox{\frakiii S}}$, es decir, es también abierto en $\cal E$ se tiene $U=V$ y $\tilde \varphi = \varphi$ y en este caso la definición 4.6.6 se reduce a la definición 4.5.2 (permanencia de la definición).

Observación 2

Sea $V$ un abierto de segunda especie en $\overline{ \mbox{\frakiii S}}$ y $\varphi \colon V \to \cal F$ una aplicación de clase $C^1$. Sea $U$ un abierto de $\cal E$ tal que $V = U \cap \overline{\mbox{\frakiii S}}$ y $\tilde \varphi$ una ampliación de clase $C^1$ de $\varphi$ a $U$. Sea $p$ un punto arbitrario de $V \cap \cal H$. Sabemos que:

$$\partial_{\vec u} {\tilde \varphi} (p) = \left\{ \begin{arra... ...1cm}\ -\vec u\mbox{ apunta hacia \frakiii S} \end{array}\right.$$

En ambos casos la derivada $\partial_{\vec u} \tilde \varphi (p)$ depende solamente de $\varphi$ y no de la ampliación $\tilde \varphi$.

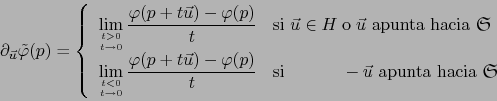
De ahí se sigue que si $\varphi \colon V \to \cal F$ es de clase $C^k$ ( $k \in {\mathbb{N}}\cup \{ \infty \}$), si también $U$ es un abierto de $\cal E$ tal que $V = U \cap \overline{\mbox{\frakiii S}}$ y existe una ampliación $\tilde \varphi \colon U \to \cal F$ de clase $C^k$ en $U$, entonces $\forall\, r \in [\![ 1,k ]\!]$ y todo $r$-uplo $(\vec{u}_1,\ldots,\vec{u}_r)$ de vectores de $E$, la derivada $\partial_{\vec{u}_1,\ldots,\vec{u}_r} \tilde \varphi (p) \;\; \forall \, p \in V$ depende solamente de $\varphi$ y no de la ampliación $\tilde \varphi$. La designamos simplemente por:

$$\partial_{\vec{u}_1,\ldots,\vec{u}_r} \varphi (p)$$

$\forall\, r \in [\![ 1,k ]\!]$ y para todos $\vec{u}_1,\ldots,\vec{u}_r \in E$ las derivadas $\partial_{\vec{u}_1,\ldots,\vec{u}_r} \varphi$ son continuas en V.

En particular si $(\vec{e}_1,\ldots,\vec{e}_n)$ es una base arbitraria en $E$, $\forall\, r \in [\![ 1,k ]\!]$ quedan bien definidas las derivadas parciales $\partial_{i_1,\ldots,i_r} \varphi$ en todos los puntos de $V$ con respecto a dicha base y son aplicaciones continuas en V.

Siguiente: Isomorfismos Arriba: Cálculo diferencial en un Anterior: La funcional