




Siguiente: Espacio vectorial tangente a
Arriba: Espacio vectorial tangente a
Anterior: Estudio del espacio vectorial
Sea  una variedad
una variedad  ,
,
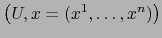 un
mapa admisible de
un
mapa admisible de  ,
, 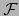 un espacio afín normado y
un espacio afín normado y 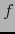 una
aplicación
una
aplicación 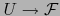 . Si para cierto punto
. Si para cierto punto 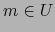 existe la
derivada parcial
existe la
derivada parcial
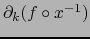 en el punto
en el punto 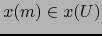 seguiremos notándola:
seguiremos notándola:
donde  es el espacio vectorial asociado con el espacio afín
es el espacio vectorial asociado con el espacio afín 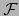 . Si esto ocurre para todo
. Si esto ocurre para todo 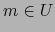 , tenemos así definida la
función
, tenemos así definida la
función
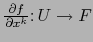 ,
función DERIVADA PARCIAL DE CON RESPECTO AL MAPA ADMISIBLE
,
función DERIVADA PARCIAL DE CON RESPECTO AL MAPA ADMISIBLE  de
de  :
:
Si
![$i_1,\ldots, i_r \in [\![ 1,n ]\!]$](img5222.png) , podemos considerar, por
reiteración, la derivada parcial:
, podemos considerar, por
reiteración, la derivada parcial:
y eventualmente la función
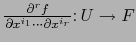 , si existen.
, si existen.
Supongamos que existe en 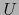 la derivada parcial segunda:
la derivada parcial segunda:
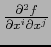 .
.
A fortiori existe:
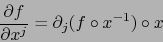 |
(12) |
La existencia de
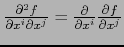 equivale
por definición a la de
equivale
por definición a la de
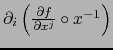 es decir, por (12), a la de
es decir, por (12), a la de
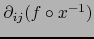 en
en 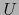 . Finalmente:
. Finalmente:
o sea:
Más generalmente:
Demostración
Procediendo por inducción, supongamos el resultado ya probado para
 (
(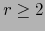 ). Supongamos que existe
). Supongamos que existe
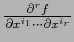 en
en 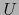 . A fortiori existe
. A fortiori existe
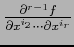 , luego por hipótesis de inducción existe
, luego por hipótesis de inducción existe
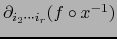 en
en 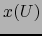 y vale:
y vale:
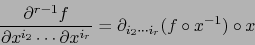 |
(13) |
Decir que existe
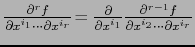 entraña (mediante (13)) que existe:
entraña (mediante (13)) que existe:
y vale:
El recíproco se prueba análogamente.

De los teoremas 6.1.7 y 4.5.8 se sigue sin más:





Siguiente: Espacio vectorial tangente a
Arriba: Espacio vectorial tangente a
Anterior: Estudio del espacio vectorial
Guillermo M. Luna
2009-06-14
![]() una variedad
una variedad ![]() ,
,
![]() un
mapa admisible de
un
mapa admisible de ![]() ,
, ![]() un espacio afín normado y
un espacio afín normado y ![]() una
aplicación
una
aplicación ![]() . Si para cierto punto
. Si para cierto punto ![]() existe la
derivada parcial
existe la
derivada parcial
![]() en el punto
en el punto ![]() seguiremos notándola:
seguiremos notándola:
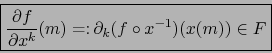
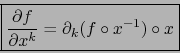
![]() la derivada parcial segunda:
la derivada parcial segunda:
![]() .
. 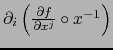 es decir, por (12), a la de
es decir, por (12), a la de
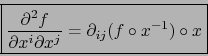

![]() (
(![]() ). Supongamos que existe
). Supongamos que existe
![]() en
en ![]() . A fortiori existe
. A fortiori existe
![]() , luego por hipótesis de inducción existe
, luego por hipótesis de inducción existe
![]() en
en ![]() y vale:
y vale:
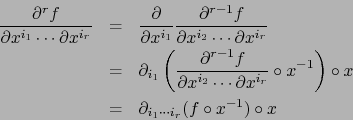
![]() y
y
![]() vale:
vale:
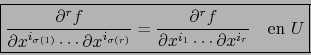
![\begin{displaymath}\fbox{${\displaystyle {\partial^2 f \over \partial x^i \parti...
...^j \partial x^i } \quad \forall \, i,\, j
\in [\![ 1,n ]\!] }$}\end{displaymath}](img5247.png)