Sean ![]() una variedad con borde y
una variedad con borde y ![]() . Imitando la definición al
comienzo de este capítulo designamos por
. Imitando la definición al
comienzo de este capítulo designamos por ![]() el conjunto
de todas las FUNCIONES LOCALES EN EL PUNTO
el conjunto
de todas las FUNCIONES LOCALES EN EL PUNTO ![]() sobre
sobre ![]() , es decir
funciones
, es decir
funciones
![]() donde
donde ![]() es una vecindad abierta de
es una vecindad abierta de ![]() en
en ![]() (que depende de
(que depende de ![]() ). Consideramos los subconjuntos
). Consideramos los subconjuntos ![]() ,
, ![]() ,
,
![]() (
(![]() ) de funciones
locales en
) de funciones
locales en ![]() respectivamente continuas en
respectivamente continuas en ![]() , diferenciables en
, diferenciables en ![]() (según la definición 5.5.8), de clase
(según la definición 5.5.8), de clase ![]() en su dominio (según la
definición 5.5.9). Vale:
en su dominio (según la
definición 5.5.9). Vale:
SiImitando la definición 6.1.1, designamos por,
y
se tiene
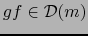
Patentemente, como antes, ![]() es un espacio vectorial real. Se llama
el ESPACIO VECTORIAL TANGENTE A LA VARIEDAD CON BORDE EN EL PUNTO . Sus elementos son los VECTORES TANGENTES A LA VARIEDAD CON BORDE EN EL PUNTO .
es un espacio vectorial real. Se llama
el ESPACIO VECTORIAL TANGENTE A LA VARIEDAD CON BORDE EN EL PUNTO . Sus elementos son los VECTORES TANGENTES A LA VARIEDAD CON BORDE EN EL PUNTO .
Para dichos vectores tangentes sigue en fuerza el teorema 6.1.2 (``LOCALIZACIÓN DE VECTORES TANGENTES''). La demostración correspondiente no sufre ningún cambio.
Si ![]() es una vecindad abierta de un punto
es una vecindad abierta de un punto ![]() de
de ![]() , se define, como
arriba, los conjuntos
, se define, como
arriba, los conjuntos
![]() ,
,
![]() ,
,
![]() ,
,
![]() de funciones locales en el punto
de funciones locales en el punto ![]() sobre la
subvariedad abierta
sobre la
subvariedad abierta ![]() de
de ![]() .
.
Sigue válido sin cambio (y con la misma demostración) el teorema
6.1.3 que permite identificar por un isomorfismo canónico los
espacios vectoriales ![]() y
y ![]() .
.
Sigue también cierto sin modificación esencial el teorema 6.1.4 que aquí reza:
Ahora aplicamos el teorema 4.6.8 (el TEOREMA DE ELLIS PARA SEMIESPACIOS CERRADOS).
Según éste la aplicación
![]() es un isomorfismo lineal canónico de
es un isomorfismo lineal canónico de
![]() sobre el espacio
vectorial tangente
sobre el espacio
vectorial tangente
![]() . Combinando con el
isomorfismo
. Combinando con el
isomorfismo
![]() obtenemos un isomorfismo inducido por
nuestro mapa de
obtenemos un isomorfismo inducido por
nuestro mapa de
![]() sobre el espacio vectorial tangente
sobre el espacio vectorial tangente ![]() .
.
De ahí la primera conclusión:
En segundo lugar:
El isomorfismo de Ellis transforma la base natural
![]() de
de
![]() en la base
en la base
A su vez las funcionales
![]() definidas por:
definidas por:
![\begin{displaymath}\fbox{${\displaystyle {\partial \over \partial x^k}(m) = \col...
...^{-1}
\partial_k (x(m)) \quad \forall \, k \in [\![ 1,n ]\!]}$}\end{displaymath}](img5262.png)
Como en el caso de variedades sin borde, obtenemos:
![]() :
:
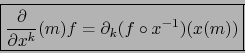
Si M es una-variedad
con borde y
es un mapa admisible de M en un punto m, vale
:
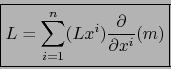
Las definiciones de derivadas parciales de orden superior con respecto a una mapa admisible y los teoremas 6.1.7 y 6.1.8 se generalizan sin más.
Como muestra, establezcamos
![]() la
fórmula:
la
fórmula:
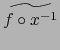 de clase
de clase
Por el teorema de Schwarz tenemos: