Siguiente: Estudio del espacio vectorial Arriba: Cálculo diferencial en variedades Anterior: Cálculo diferencial en variedades

Espacio vectorial tangente a una variedad diferenciable en un punto

Espacio vectorial tangente en un punto

El cálculo diferencial en espacios afines normados estriba en gran parte en la posibilidad de combinar allí operaciones con puntos y vectores. Pero hasta el momento no disponemos en variedades diferenciables de entes análogos a vectores. Aunque no parezca factible la construcción para una variedad diferenciable de algo como el espacio vectorial asociado a un espacio afín, la clave de la solución está en el teorema de Ellis (teorema 4.3.10). Éste afirma que el espacio vectorial tangente ${\cal E}_m$ en cualquier punto $m$ de un espacio afín de dimensión finita es canónicamente isomorfo con el espacio vectorial $E$ asociado con $\cal E$. Ahora bien, augurio feliz, la definición de vectores tangentes en un punto de $\cal E$ puede trasponerse tal cual a una variedad diferenciable.

Sea $M$ una variedad $C^k$ $(k \in {\mathbb{N}}\cup \{ \infty \})$ y $m$ un punto de $M$. Exactamente como para un espacio afín designaremos por ${\cal F}(m)$ el conjunto de todas las FUNCIONES LOCALES en $m$, es decir, las funciones $f \colon V \to {\mathbb{R}}$, donde $V$ es una vecindad abierta de $m$ que depende de $f$; designamos por ${\cal C}(m)$ el conjunto de las funciones locales en $m$, continuas en $m$ y por ${\cal D}(m)$ el conjunto de las funciones locales en $m$, diferenciables en m. Si $j \in [\![ 1, k ]\!]$ designaremos por ${\cal C}^j (m)$ el conjunto de las funciones locales en $m$ que son, cada una de clase $C^j$ en su dominio.

Si $f\in {\cal F}(m)$ designamos por $\mbox{\rm Dom } f$ el dominio de la función $f$. En ${\cal F}(m)$ definimos una adición y una multiplicación exactamente como en la definición 4.3.2. Los conjuntos ${\cal C}(m),\, {\cal D}(m), {\cal C}^j (m)$ son cerrados con respecto a estas operaciones.

También en virtud del teorema 5.2.6:

Si $f \in {\cal D}(m), \, f(m) = 0$ y $g \in {\cal C}(m)$ vale $fg \in {\cal D}(m)$.

Definición 1.1   Sea $M$ una variedad $C^k$ $(k \in {\mathbb{N}}\cup \{ \infty \})$ y $m$ un punto de $M$. Una funcional $L \colon {\cal D}(m) \to {\mathbb{R}}$ se llama VECTOR TANGENTE A LA VARIEDAD $M$ en el punto $m$, si goza de las tres ``propiedades leibnizianas'', a saber:

$$\fbox{${\displaystyle \begin{array}{rcl} \mbox{1}) && L(\alph... ...\rm \ y\ } g \in {\cal C}(m): L (fg) = g(m) L f \end{array}}$}$$

Teorema 1.1 (y definición)   El conjunto de los vectores tangentes en un punto $m$ de una variedad $m$ es un espacio vectorial real. Se designa por $M_m$. Se llama el ESPACIO VECTORIAL TANGENTE A LA VARIEDAD EN EL PUNTO $m$.

Este resultado (por cierto inmediato) se demuestra exactamente como el teorema 4.3.9.

Teorema 1.2  

1. Si $V$ es una vecindad abierta de $m$ en $M$, $1_V$ la función $V \to {\mathbb{R}}$ constante de valor $1$ y $\alpha \in {\mathbb{R}}$, vale $\forall \, L \in M_m$:
   
   $$\fbox{${\displaystyle L ( \alpha \, 1_V) = 0}$}$$
   
   
   ($\alpha \, 1_V$ es la función $V \to {\mathbb{R}}$ constante de valor $\alpha$).
2. $\forall \, f \in {\cal D}(m)$ vale:
   
   $$\fbox{${\displaystyle L (1_V f) = L f}$}$$
   
   
   ($1_V f$ es la restricción de $f$ a la vecindad abierta $V \cap \mbox{\rm Dom } f$ de $m$).
3. PRINCIPIO DE LOCALIZACIÓN DE VECTORES TANGENTES: Si dos funciones $f,\, g \in {\cal D}(m)$ coinciden en cierta vecindad de $m$ entonces vale $Lf = Lg\; \forall \, L \in M_m$.

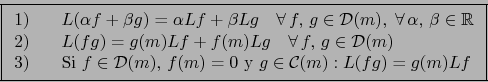
Demostración

1. La afirmación a) se muestra exactamente como la correspondiente observación después del teorema 4.3.9, a saber:

   Por la propiedad leibniziana 2) de $L$ vale:
   

   $$L(1_V) = L (1_V^2)= 2\, 1_V(m)L(1_V) = 2L\, 1_V$$
   
   
   de donde $L(1_V)=0$. También por la propiedad leibniziana 1) de $L$: $L( \alpha\, 1_V) = \alpha L (1_V) = \alpha \cdot 0 = 0$.
2. Si $f\in {\cal D}(m)$, vale por la propiedad leibniziana 2) de $L$:
   
   $$L(1_V \, f)= 1_V(m) L f + f(m) L (1_V)$$
   
   
   o sea, usando a): $L(1_V \, f) = 1\cdot Lf= Lf$.
3. Supongamos que las funciones $f,\, g \in {\cal D}(m)$ coinciden en cierta vecindad abierta $W$ de $m$. Por el inciso b):
   
   $$L f = L (1_W \, f) \quad {\rm y} \quad Lg= L(1_W \, g)$$
   
   
   Pero por hipótesis $1_W \, f = 1_W\, g$, luego: $Lf = Lg$. $\quad\Box$

Notaciones

Sea $M$ una variedad $C^k \,(k \in {\mathbb{N}}\cup \{ \infty \} )$, m en un punto de $M$ y $U$ una vecindad abierta (fija) del punto $m$ en $M$. $U$ es también una variedad $C^k$, a saber, una subvariedad abierta de $M$. Designamos por ${\cal F}_U (m)$ el conjunto de las FUNCIONES LOCALES EN SOBRE , es decir, de las funciones $f \colon V \to {\mathbb{R}}$ donde $V$ es una vecindad abierta de $m$ con respecto a $U$, o sea, una vecindad abierta de $m$ en $M$ contenida en $U$, que depende de $f$. Designamos por ${\cal C}_U(m)$ (resp. ${\cal D}_U (m)$) el conjunto de todas las funciones locales en $m$ sobre $U$ continuas (resp. diferenciables) en el punto $m$.

Claramente:

$${\cal F}_U (m) \subset {\cal F}(m)\quad , \quad {\cal C}_U (m... ...al C}(m) \quad {\rm y} \quad {\cal D}_U (m) \subset {\cal D}(m)$$

Finalmente, designamos por $U_m$ el espacio vectorial tangente a la variedad $U$ en el punto $m$, vale decir el espacio vectorial de todas las funcionales ${\cal D}_{U(m)} \to {\mathbb{R}}$ que posee las propiedades leibnizianas 1), 2), 3).

Teorema 1.3   Para cada $L \in M_m$, sea $L_U$ la restricción de la funcional $L \colon {\cal D}(m) \to {\mathbb{R}}$ al subconjunto ${\cal D}_U (m)$ de ${\cal D}(m)$.

La aplicación $L \mapsto L_U$ es un isomorfismo lineal (canónico) del espacio vectorial $M_m$ tangente a $M$ en el punto $m$ sobre el espacio vectorial $U_m$ tangente a la variedad $U$ en el punto $m$.

Dicho isomorfismo lineal puede usarse para identificar los dos espacios vectoriales tangentes. Escribiremos simplemente:

$$\fbox{${\displaystyle U_m \approx M_m}$}$$

Demostración
Es claro que $\forall \, L \in M_m$ su restricción $L_U$ es un elemento de $U_m$ y que la aplicación $L \mapsto L_U$ es una aplicación lineal del espacio vectorial $M_m$ en el espacio vectorial $U_m$.

1. Supongamos $L_U = 0$. Sea $f$ un elemento arbitrario de ${\cal D}(m)$. Por el teorema 6.1.2 inciso b) vale:
   
   $$Lf = L (1_U \, f) = L_U (1_U \, f) = 0$$
   
   
   donde $L= 0$. Luego la aplicación $L \mapsto L_U$ es inyectiva.
2. Sea $l \in U_m$ arbitrario. Definamos una funcional $L \colon {\cal D}(m) \to {\mathbb{R}}$, poniendo $\forall \, f \in {\cal D}(m)$:
   
   $$L f= \colon l (1_U \, f)$$
   
   
   Puesto que $1_U\, f \in {\cal D}_U (m)$ se ve inmediatamente que $L \in M_m$ y que $l$ es la restricción de $L$ a ${\cal D}_U (m)$, o sea:
   
   $$l = L_U$$
   
   
   La aplicación lineal $L \mapsto L_U$ es, pues, superyectiva. $\quad\Box$

Siguiente: Estudio del espacio vectorial Arriba: Cálculo diferencial en variedades Anterior: Cálculo diferencial en variedades