Usando mapas admisibles vamos a obtener resultados de importancia decisiva sobre espacios vectoriales tangentes.
Sea M una variedad
![]() y sea
y sea ![]() un
punto de
un
punto de ![]() . Sea
. Sea
![]() . Usamos un mapa admisible
. Usamos un mapa admisible
![]() de la variedad
de la variedad ![]() en el punto
en el punto ![]() y
nos fijamos en las subvariedades abiertas
y
nos fijamos en las subvariedades abiertas ![]() de
de ![]() y
y ![]() de
de
![]() .
.
Si
![]() entonces vale
entonces vale
![]() . Por cierto la aplicación:
. Por cierto la aplicación:
También debido a la definición 5.2.2 y a la demostración del teorema 5.2.5, la restricción de la biyección (1) a
![]() es una
biyección de
es una
biyección de ![]() sobre
sobre
![]() .
.
Demostración
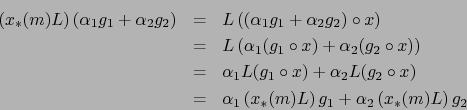
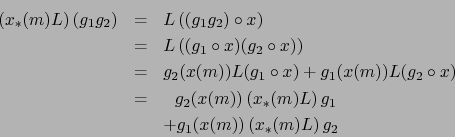
Así pues,
![]() como afirmamos.
como afirmamos.
Claramente, ![]() es una aplicación lineal de
es una aplicación lineal de ![]() en
en
![]() y
y
![]() es una aplicación lineal de
es una aplicación lineal de
![]() en
en ![]() .
.
El simple teorema 6.1.4 combinado con el teorema de Ellis (teorema 4.3.10) conduce a las siguientes observaciones muy importantes.
Observación 1
Usando las identificaciones:
Pero por el teorema de Ellis, el espacio vectorial
![]() es a su vez canónicamente isomorfo al espacio vectorial
es a su vez canónicamente isomorfo al espacio vectorial
![]() . Luego
. Luego ![]() puede considerarse como isomorfismo lineal
de
puede considerarse como isomorfismo lineal
de ![]() sobre
sobre
![]() . En particular
. En particular
![]() , o sea:
, o sea:
Observación 2
Sea
![]() la base natural de
la base natural de
![]() . El
isomorfismo
. El
isomorfismo
![]() del teorema de Ellis identifica
del teorema de Ellis identifica
![]() con la funcional:
con la funcional:
Al considerar
![]() como isomorfismo
como isomorfismo
![]() tendremos pues:
tendremos pues:
Las funcionalesExplicitemos las funcionalesconstituyen una base del espacio vectorial
tangente a la variedad
en el punto
. Se llama la BASE DE INDUCIDA POR EL MAPA ADMISIBLE
de la variedad
en el punto
.
Si ![]() es un mapa admisible de
es un mapa admisible de ![]() y
y
![]() es una
función diferenciable en
es una
función diferenciable en ![]() , la fórmula (10) define una función
, la fórmula (10) define una función
![]() , la FUNCIÓN DERIVADA PARCIAL CON RESPECTO LA -ÉSIMA COORDENADA LOCAL. Al quitar
el argumento
, la FUNCIÓN DERIVADA PARCIAL CON RESPECTO LA -ÉSIMA COORDENADA LOCAL. Al quitar
el argumento ![]() en (10) obtenemos:
en (10) obtenemos:
Nota
Notemos que si
![]() ,
,
![]() son dos mapas admisibles de
son dos mapas admisibles de ![]() de dominio
de dominio ![]() y
y
![]() es una función diferenciable en
es una función diferenciable en ![]() , se puede
hablar en toda corrección de funciones
, se puede
hablar en toda corrección de funciones
![]() y
y
![]() en
en ![]() como ya
hacía Leibniz, cuyas maravillosas notaciones siguen, como veremos
más adelante, correctas, pese a unas críticas en el pasado,
debidas a la incapacidad de bien interpretarlas.
como ya
hacía Leibniz, cuyas maravillosas notaciones siguen, como veremos
más adelante, correctas, pese a unas críticas en el pasado,
debidas a la incapacidad de bien interpretarlas.
Demostración
Designemos por
![]() ,
,
![]() , las
``proyecciones naturales'':
, las
``proyecciones naturales'':
Por el teorema de Ellis vale
![]() :
:
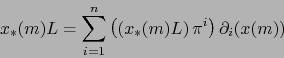
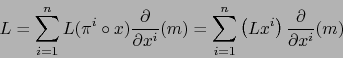
Demostración
En efecto, si
![]() es un mapa
admisible en
es un mapa
admisible en ![]() , en virtud del teorema 6.1.5, para conocer
, en virtud del teorema 6.1.5, para conocer ![]() basta conocer los números
basta conocer los números ![]() ,
, ![]() y
y ![]() son
funciones de clase
son
funciones de clase ![]() .
.
![]()
Demostración
Usando la fórmula (10) de la observación 2 conseguimos:
Nota
Existen diferentes métodos para definir y estudiar el espacio vectorial
tangente en un punto de una variedad diferenciable. El que elegimos se
debe al profesor H. G. ELLIS [16] de la Universidad de Colorado.
Las tentativas de definir los vectores tangentes a ![]() en un punto
en un punto ![]() como funcionales convencionales sobre cierto tipo de funciones locales
en
como funcionales convencionales sobre cierto tipo de funciones locales
en ![]() no son nuevas.
En el tomo I de su tratado de grupos de Lie [10], el matemático francés
CLAUDE CHEVALLEY supone que
no son nuevas.
En el tomo I de su tratado de grupos de Lie [10], el matemático francés
CLAUDE CHEVALLEY supone que ![]() es una variedad analítica y define
vectores tangentes a
es una variedad analítica y define
vectores tangentes a ![]() en
en ![]() como funcionales sobre el conjunto
como funcionales sobre el conjunto
![]() de funciones locales en
de funciones locales en ![]() , cada una analítica en su
dominio, postulando que dichas funcionales satisfacen las propiedades
leibnizianas 1) y 2).
, cada una analítica en su
dominio, postulando que dichas funcionales satisfacen las propiedades
leibnizianas 1) y 2).
Es fácil generalizar la definición de Chevalley postulando solamente
que ![]() es una variedad
es una variedad ![]() y sustituyendo
y sustituyendo ![]() por
por
![]() , el conjunto de funciones locales en
, el conjunto de funciones locales en ![]() , cada una de
clase
, cada una de
clase ![]() en su dominio. De nuevo basta exigir que las
funcionales consideradas
en su dominio. De nuevo basta exigir que las
funcionales consideradas
![]() gocen de las propiedades
leibnizianas 1) y 2). Ellis atribuye la mencionada generalización a H. FLANDERS [17].
gocen de las propiedades
leibnizianas 1) y 2). Ellis atribuye la mencionada generalización a H. FLANDERS [17].
Desgraciadamente, si uno insiste en no usar más que las propiedades
leibnizianas 1) y 2), resulta imposible una generalización ulterior a
variedades ![]() con
con ![]() finito.
finito.
En efecto, en el año 1956 el matemático belga G. PAPY [30] probó que si
![]() es una variedad
es una variedad ![]() con
con
![]() , el espacio vectorial de las
funcionales
, el espacio vectorial de las
funcionales
![]() que satisfacen las propiedades
leibnizianas 1) y 2) es de dimensión infinita.
que satisfacen las propiedades
leibnizianas 1) y 2) es de dimensión infinita.
El mérito de Ellis fue el descubrimiento del muy simple resultado c) del teorema 4.3.5 y la consecuente añadidura de la propiedad leibniziana 3) a la definición de vectores tangentes.
El método de Ellis es muy natural y ``geométrico'', muy económico,
pues no exige más que la diferenciabilidad de funciones locales
consideradas en el solo punto ![]() (¡menos no se puede!) y
técnicamente muy cómodo (esperemos que de esto se convencerá el
lector a continuación).
(¡menos no se puede!) y
técnicamente muy cómodo (esperemos que de esto se convencerá el
lector a continuación).
Como lo hace patente nuestra redacción, ocurre el hecho (quizá sorprendente) de que el principal teorema de la teoría (teorema 4.3.10) no es un teorema sobre variedades diferenciables, sino uno sobre espacios afines de dimensión finita.