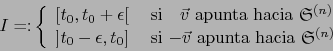Siguiente: Diferenciación
Arriba: Espacio vectorial tangente a
Anterior: Vectores tangentes a una
Volvamos un momento al espacio afín  de dimensión finita,
provisto de un referencial
de dimensión finita,
provisto de un referencial
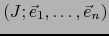 . Sea
. Sea
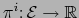 ;
;
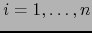 las coordenadas con
respecto a dicho referencial, es decir:
las coordenadas con
respecto a dicho referencial, es decir:
Sea
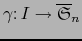 una curva en
una curva en
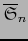 diferenciable en un tiempo
diferenciable en un tiempo 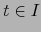 . Conocer
. Conocer
 equivale a conocer sus funciones coordenadas
equivale a conocer sus funciones coordenadas
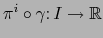 , pues:
, pues:
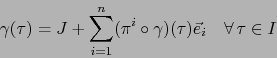 |
(21) |
Derivando en el tiempo 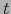 obtenemos de (21) la fórmula familiar:
obtenemos de (21) la fórmula familiar:
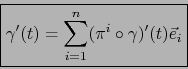 |
(22) |
Generalicemos la fórmula (22) a una curva en una variedad con borde.
Demostración
Por el teorema 6.1.5 que hemos generalizado a variedades con borde
(ver consideraciones después del teorema 6.1.9), tenemos:
Pero por definición de 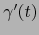 se cumple:
se cumple:
de donde la fórmula anunciada.

La razón principal para considerar vectores tangentes a curvas es que
todo vector tangente a una variedad con borde  en un punto
en un punto  de
ésta puede representarse (de muchas maneras) como un vector tangente a
una curva en
de
ésta puede representarse (de muchas maneras) como un vector tangente a
una curva en  que ``pasa por el punto
que ``pasa por el punto  ''.
''.
Vale en efecto:
Demostración
Para la precisión en los detalles nos será conveniente distinguir
tres casos:
Caso 1.
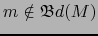 .
.
Si  es una variedad sin borde, este caso será el único por
considerar. Usamos un mapa admisible
es una variedad sin borde, este caso será el único por
considerar. Usamos un mapa admisible  de primera especie de
de primera especie de  en el punto
en el punto  . Recordamos que según nuestra terminología esto
entraña que
. Recordamos que según nuestra terminología esto
entraña que 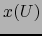 es abierto en
es abierto en
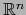 . Sea
. Sea 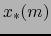 el
correspondiente isomorfismo del espacio vectorial tangente
el
correspondiente isomorfismo del espacio vectorial tangente 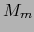 sobre
el espacio vectorial tangente
sobre
el espacio vectorial tangente
 .
.
Por el teorema de Ellis,
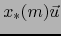 se representa únicamente
como la funcional
se representa únicamente
como la funcional
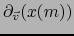 con
con
 . Por
el isomorfismo de Ellis, ésta se identifica con
. Por
el isomorfismo de Ellis, ésta se identifica con 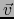 . Escribiremos
pues, simplemente:
. Escribiremos
pues, simplemente:
Por ser 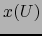 un abierto de
un abierto de
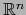 ,
,
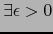 tal que:
tal que:
Sean 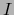 el intervalo abierto
el intervalo abierto
![$]-\epsilon + t_0 , \epsilon + t_0[$](img5351.png) y
y
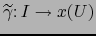 la curva en
la curva en 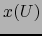 dada por:
dada por:
 es de clase
es de clase  , en particular es
diferenciable en el tiempo
, en particular es
diferenciable en el tiempo  . Se verifica:
. Se verifica:
Sea
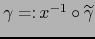 la correspondiente
curva
la correspondiente
curva 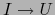 . Es de clase
. Es de clase  , a mayor abundamiento diferenciable
en el tiempo
, a mayor abundamiento diferenciable
en el tiempo  . La relación (23) entraña:
. La relación (23) entraña:
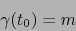 |
(25) |
Por las consideraciones heurísticas antes del teorema 6.1.10, el
vector
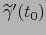 , identificado con
, identificado con
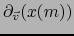 , no es otro que el vector tangente a la curva
, no es otro que el vector tangente a la curva
 en el tiempo
en el tiempo  según la definición en este teorema. Cumple:
según la definición en este teorema. Cumple:
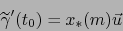 |
(26) |
Pero por el teorema 6.1.11 se verifica también:
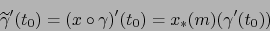 |
(27) |
Cotejando (26) con (27) obtenemos, debido a que 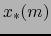 es un
isomorfismo:
es un
isomorfismo:
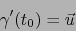 |
(28) |
Las relaciones (25) y (28) establecen el teorema en este caso.
Caso 2.
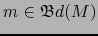 y
y
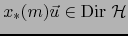 donde se tiene que el hiperplano
donde se tiene que el hiperplano
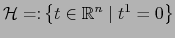 es el borde de
es el borde de
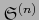 .
Como en el caso 1 ponemos:
.
Como en el caso 1 ponemos:
e identificamos 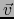 con un vector de
con un vector de
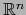 .
.
Vale
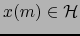 . Puesto que el conjunto
. Puesto que el conjunto
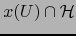 es una
vecindad abierta del punto
es una
vecindad abierta del punto  en
en 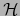 , existe
, existe 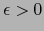 tal
que:
tal
que:
Sea 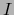 el intervalo abierto
el intervalo abierto
![$]t_0 - \epsilon , t_0 + \epsilon[$](img5373.png) .
Consideramos la curva
.
Consideramos la curva
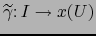 dada por:
dada por:
y su ``levantamiento''
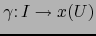 donde
donde
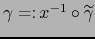 . Las particularidades del caso son que:
Como en el caso 1 vale:
. Las particularidades del caso son que:
Como en el caso 1 vale:
De ahí deducimos exactamente como en dicho caso 1:
Caso 3.
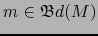 y
y
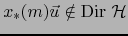 .
.
Usamos un mapa admisible  de segunda especie de
de segunda especie de  en el punto
en el punto
 .
. 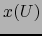 es, pues, un abierto de
es, pues, un abierto de
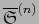 que
interseca el hiperplano
que
interseca el hiperplano 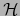 . Se verifica:
. Se verifica:
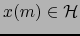 .
Como arriba ponemos:
.
Como arriba ponemos:
 e identificamos
e identificamos
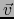 con un vector de
con un vector de
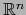 .
Existe
.
Existe 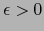 tal que:
tal que:
Si 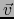 apunta hacia el semiespacio
apunta hacia el semiespacio

y si 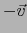 apunta hacia el semiespacio
apunta hacia el semiespacio

Definimos el intervalo:
y consideramos la curva
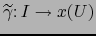 dada por:
dada por:
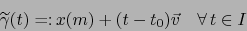 |
(29) |
 es de clase
es de clase  . A mayor abundamiento es
diferenciable en el tiempo
. A mayor abundamiento es
diferenciable en el tiempo  . Vale:
. Vale:
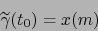 |
(30) |
y
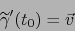 |
(31) |
Como arriba, consideramos la curva
 . Es de clase
. Es de clase  . Por (30) vale:
. Por (30) vale:
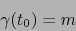 |
(32) |
Usando como en el caso 1 las consideraciones heurísticas antes del
teorema 6.1.10 y el teorema 6.1.11 hallamos de nuevo
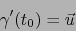 |
(33) |
Las fórmulas (32) y (33) concluyen la prueba del teorema.






Siguiente: Diferenciación
Arriba: Espacio vectorial tangente a
Anterior: Vectores tangentes a una
Guillermo M. Luna
2009-06-14
![]() de dimensión finita,
provisto de un referencial
de dimensión finita,
provisto de un referencial
![]() . Sea
. Sea
![]() ;
;
![]() las coordenadas con
respecto a dicho referencial, es decir:
las coordenadas con
respecto a dicho referencial, es decir:
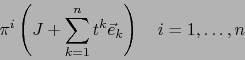
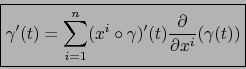
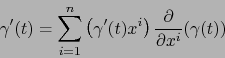
![]() en un punto
en un punto ![]() de
ésta puede representarse (de muchas maneras) como un vector tangente a
una curva en
de
ésta puede representarse (de muchas maneras) como un vector tangente a
una curva en ![]() que ``pasa por el punto
que ``pasa por el punto ![]() ''.
''.
![]() .
.
![]() es una variedad sin borde, este caso será el único por
considerar. Usamos un mapa admisible
es una variedad sin borde, este caso será el único por
considerar. Usamos un mapa admisible ![]() de primera especie de
de primera especie de ![]() en el punto
en el punto ![]() . Recordamos que según nuestra terminología esto
entraña que
. Recordamos que según nuestra terminología esto
entraña que ![]() es abierto en
es abierto en
![]() . Sea
. Sea ![]() el
correspondiente isomorfismo del espacio vectorial tangente
el
correspondiente isomorfismo del espacio vectorial tangente ![]() sobre
el espacio vectorial tangente
sobre
el espacio vectorial tangente
![]() .
.
![]() se representa únicamente
como la funcional
se representa únicamente
como la funcional
![]() con
con
![]() . Por
el isomorfismo de Ellis, ésta se identifica con
. Por
el isomorfismo de Ellis, ésta se identifica con ![]() . Escribiremos
pues, simplemente:
. Escribiremos
pues, simplemente:
![]() y
y
![]() donde se tiene que el hiperplano
donde se tiene que el hiperplano
![]() es el borde de
es el borde de
![]() .
Como en el caso 1 ponemos:
.
Como en el caso 1 ponemos:
![]() . Puesto que el conjunto
. Puesto que el conjunto
![]() es una
vecindad abierta del punto
es una
vecindad abierta del punto ![]() en
en ![]() , existe
, existe ![]() tal
que:
tal
que:
![]() y
y
![]() .
.
![]() de segunda especie de
de segunda especie de ![]() en el punto
en el punto
![]() .
. ![]() es, pues, un abierto de
es, pues, un abierto de
![]() que
interseca el hiperplano
que
interseca el hiperplano ![]() . Se verifica:
. Se verifica:
![]() .
Como arriba ponemos:
.
Como arriba ponemos:
![]() e identificamos
e identificamos
![]() con un vector de
con un vector de
![]() .
Existe
.
Existe ![]() tal que:
tal que:
![]() apunta hacia el semiespacio
apunta hacia el semiespacio
![]()