Siguiente: Bibliography Arriba: Diferenciación Anterior: Diferenciales y curvas

Diferenciales de funciones reales

Nota
Sean $M$ una variedad $C^k$ con borde y $f \colon M \to {\mathbb{R}}$ una función diferenciable en un punto $m \in M$. Al considerar la diferencial $df(m) \colon M_m \to {\mathbb{R}}_{f(m)}$ identificamos siempre, conforme al teorema de Ellis, ${\mathbb{R}}$ con el espacio ${\mathbb{R}}_{f(m)}$ tangente a ${\mathbb{R}}$ en el punto $f(m)$. Ver lo redactado a este respecto en la observación preliminar al teorema 6.2.4.

Debido a este convenio $df(m)$ será una aplicación lineal de $M_m$ en ${\mathbb{R}}$ elemento del espacio $M_m^\ast$, dual del espacio $M_m$.

$$\fbox{${\displaystyle df(m) \in M_m^\ast}$}$$

Teorema 2.6   Sean $M$ una variedad $C^k$ con borde y $f \colon M \to {\mathbb{R}}$ una función diferenciable en un punto $m \in M$.

Mediante el convenio $df(m) \in M_m^\ast$ se verifica:

$$\fbox{${\displaystyle \left\langle \vec u , df(m) \right\rangle = \vec u \cdot f \quad \forall \, \vec u \in M_m}$}$$

Primera demostración

Al considerar $\left\langle \vec u, df(m) \right\rangle$ como funcional $L \colon {\cal D}(f(m)) \to {\mathbb{R}}$, tenemos,

$$\forall \, g \in {\cal D}(f(m)):\ \ L \cdot g = \vec u \cdot (g \circ f).$$

Por la observación preliminar al teorema 6.2.4 $L$ se identifica con el número real $L ({\cal I}_{{\mathbb{R}}} ) = \vec u \cdot ( {\cal I}_{{\mathbb{R}}} \circ f) = \vec u \cdot f$. $\quad\Box$

Segunda demostración

Sea $\vec u \in M_m$. Aplicando el teorema 6.1.13, obtenemos una curva $\gamma \colon I \to M$ diferenciable en un tiempo $t \in I$ tal que:

$$\gamma(t) = m \quad {\rm y}\quad \gamma' (t) = \vec u$$

Por el teorema 6.2.5 se cumple:

$$\left\langle \vec u , d f(m) \right\rangle = \left\langle \gamma' (t), df( \gamma(t)) \right\rangle = (f \circ \gamma)'(t)$$

donde $(f \circ \gamma)' \in {\mathbb{R}}_{f(m)}$ se identifica con el número real:

$$(f \circ \gamma)'(t) = \gamma'(t) \cdot f = \vec u \cdot f$$

$\quad\Box$

Teorema 2.7   Sean $M$ una variedad $C^k$ con borde y $m$ un punto de $M$

1. Si $f,\, g \colon M \to {\mathbb{R}}$ son funciones diferenciables en el punto $m$, vale $\forall \, \alpha,\, \beta \in {\mathbb{R}}$:
   
   $$\fbox{${\displaystyle d (\alpha f + \beta g) (m) = \alpha df(m) + \beta dg(m)}$}$$
   
   

2. Si $f,\, g \colon M \to {\mathbb{R}}$ son funciones diferenciables en el punto $m$, vale:
   
   $$\fbox{${\displaystyle d (f g) (m) = g(m) df(m) + f(m) dg(m)}$}$$
   
   

3. Si $f \colon M \to {\mathbb{R}}$ es diferenciable en $m$, satisface $f(m) =0$ y $g \colon M \to {\mathbb{R}}$ es continua en $m$, vale:
   
   $$\fbox{${\displaystyle d (f g) (m) = g(m) df(m)}$}$$
   
   

Demostración
Las relaciones enunciadas siguen sin más del teorema 6.2.6 y de las propiedades leibnizianas de los vectores de $M_m$. Como muestra probemos, por ejemplo, explícitamente la afirmación b).

Si $f,\, g \colon M \to {\mathbb{R}}$ son funciones diferenciables en $m$ y $\vec u \in M_m$ se verifica por el teorema 6.2.6:

$$\begin{eqnarray*} \left\langle \vec u , d(fg)(m) \right\rangle &=& \vec u \cdot ... ...\ &=& \left\langle\vec u, g(m) df(m)+ f(m)dg(m) \right\rangle \end{eqnarray*}$$

$\quad\Box$

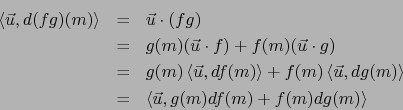
He aquí un resultado complementario.

Teorema 2.8   Sean $M$ una variedad $C^k$ con borde y $m$ un punto de $M$. Si $f \colon M \to {\mathbb{R}}$ y $g \colon M \to {\mathbb{R}}-\{ 0 \}$ son funciones diferenciables en el punto $m$, la función ${ {f \over g} \colon M \to {\mathbb{R}}}$ es diferenciable en $m$ y cumple:

$$\fbox{${\displaystyle d { f\over g} (m) = {g(m) df(m) - f(m) dg(m) \over g(m)^2}}$}$$

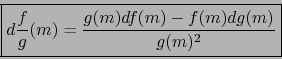
Demostración

1. Sea ${\cal I}^{-1} \colon {\mathbb{R}}-\{ 0 \} \to {\mathbb{R}}$ la función ${ t \mapsto {1 \over t}}$. Esta función es derivable, equivalentemente diferenciable en todo punto del abierto ${\mathbb{R}}- \{ 0 \}$ de ${\mathbb{R}}$. Vale $\forall \, t \in {\mathbb{R}}- \{ 0 \}$ y $\forall \, h \in {\mathbb{R}}$:
   

   $$d{\cal I}^{-1} (t) (h) = {- h \over t^2}$$ (6)

   
   
   Puesto que $g$ es diferenciable en $m$, $g(m) \ne 0$ y ${\cal I}^{-1}$ es diferenciable en virtud del teorema 5.5.7 la función:
   

   $${1 \over g} = {\cal I}^{-1} \circ g$$ (7)

   
   
   es diferenciable en $m$.

   Por la regla de la cadena (teorema 6.2.2) aplicada a (7) conseguimos $\forall \, \vec u \in M_m$:
   

   $$\left\langle \vec u, \left(d{1 \over g} \right) (m) \right\ra... ...t) = - { \left\langle \vec u, dg(m) \right\rangle \over g(m)^2}$$
   
   
   o sea
   

   $$\left( d{1 \over g} \right) (m) = - {dg(m) \over g(m)^2}$$ (8)

   
   

2. Considerando la fórmula (8) con el inciso b) del teorema 6.2.7 conseguimos finalmente:
   $$\begin{eqnarray*} \left( d {f \over g} \right) (m) &=& d \left( f \cdot {1 \over... ...m) \over g(m)^2} \\ &=& {g(m) df(m) - f(m)dg(m) \over g(m)^2} \end{eqnarray*}$$
   
   

$\quad\Box$

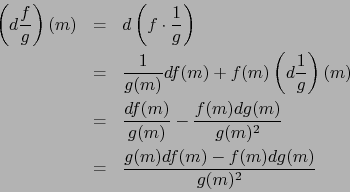
Con esto damos por concluida nuestra exposición introductoria a las variedades diferenciables.

Siguiente: Bibliography Arriba: Diferenciación Anterior: Diferenciales y curvas