




Siguiente: Aplicaciones de clase
Arriba: Variedades con borde
Anterior: Producto de una variedad
Definición 5.8
Sean  ,
,  variedades con borde de clase
variedades con borde de clase  de sendas dimensiones
de sendas dimensiones  ,
,  y
y  una aplicación
una aplicación 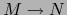 . Se dice que la aplicación
. Se dice que la aplicación
 es DIFERENCIABLE en un punto
es DIFERENCIABLE en un punto 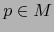 si existen mapas
admisibles
si existen mapas
admisibles  de
de  en el punto p (en
en el punto p (en
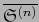 ) y
) y  de
de  en el punto
en el punto  (en
(en
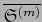 ) tales que
) tales que
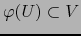 y la
aplicación
y la
aplicación
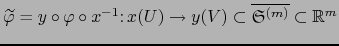 (``
(`` leída en los mapas considerados'') es diferenciable en el punto
leída en los mapas considerados'') es diferenciable en el punto
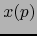 según la definición 4.6.1.
según la definición 4.6.1.
Observación (Carácter local de la diferenciación)
Sean  ,
,  variedades
variedades  con bordes y
con bordes y  una aplicación
una aplicación
 . Sean
. Sean  un punto de
un punto de  y
y 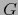 una vecindad abierta de
una vecindad abierta de  en
en
 .
.  es diferenciable en el punto
es diferenciable en el punto  , si y sólo si la
restricción
, si y sólo si la
restricción 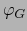 de
de  a la subvariedad abierta
a la subvariedad abierta 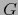 de
de
 es diferenciable en el punto
es diferenciable en el punto  .
.
Demostración
Sean
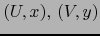 mapas admisibles de sendas variedades con bordes
mapas admisibles de sendas variedades con bordes
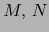 en sendos puntos
en sendos puntos
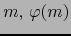 tales que
tales que 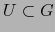 y
y
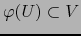 .
Decir que
.
Decir que  es diferenciable en
es diferenciable en  significa que:
significa que:
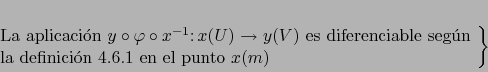 |
(11) |
Pero  es también un mapa admisible de la subvariedad abierta
es también un mapa admisible de la subvariedad abierta
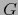 de
de  en el punto
en el punto  .
.
Así pues, la afirmación (11) significa también que la
restricción 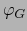 es diferenciable en
es diferenciable en  .
.

He aquí un teorema análogo al teorema 5.2.3 que hace
manejable la definición precedente.
Teorema 5.6
Si
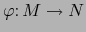 es una aplicación diferenciable en un
punto
es una aplicación diferenciable en un
punto 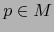 , para todo par de mapas admisibles
, para todo par de mapas admisibles
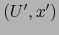 de
de  en
en  ,
,
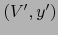 de
de  en
en  tales que
tales que
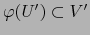 la aplicación
la aplicación
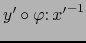 de
de
 en
en
 es diferenciable en el punto
es diferenciable en el punto
 según la definición 4.6.5.
según la definición 4.6.5.
Demostración
Ponemos
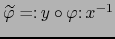 .
Restringimos
.
Restringimos 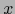 y
y 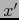 a
a
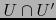 . Por hipótesis
. Por hipótesis
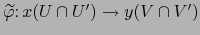 es diferenciable en el punto
es diferenciable en el punto 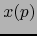 según la definición 4.6.5.
según la definición 4.6.5.
 leída en los mapas
leída en los mapas
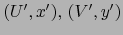 es la aplicación:
es la aplicación:
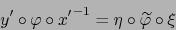 |
(12) |
donde:
son los cambios de mapas.
Éstos son isomorfismos  según las definiciones 4.6.6 y 4.6.7.
Existen, pues, un abierto
según las definiciones 4.6.6 y 4.6.7.
Existen, pues, un abierto 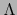 del espacio real
del espacio real
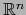 tal que
tal que
 , un abierto
, un abierto 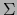 de
de
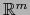 tal que
tal que
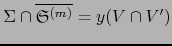 , una aplicación
, una aplicación 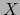 de clase
de clase  (en el sentido C.D.):
(en el sentido C.D.):
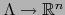 , ampliación de
, ampliación de 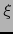 y una aplicación
y una aplicación
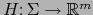 de clase
de clase  (en el sentido C.D.), ampliación de
(en el sentido C.D.), ampliación de
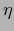 .
También en virtud de la definición 4.6.6 existe un abierto
.
También en virtud de la definición 4.6.6 existe un abierto 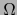 de
de
 tal que
tal que
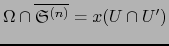 y una aplicación
y una aplicación
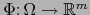 ,
ampliación de
,
ampliación de
 , diferenciable C.D. en
, diferenciable C.D. en 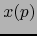 .
.
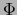 es a fortiori continua en el punto
es a fortiori continua en el punto 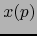 y se verifica
y se verifica
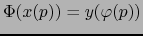 . Puesto que
. Puesto que 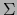 es una vecindad del punto
es una vecindad del punto
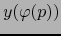 en
en
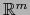 , por continuidad existe una vecindad abierta
, por continuidad existe una vecindad abierta
 de
de 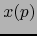 en
en
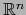 contenida en
contenida en 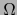 tal que
tal que
 .
.
La aplicación 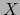 , por ser de clase
, por ser de clase  es a fortiori continua en
es a fortiori continua en
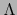 . Luego
. Luego
 es una vecindad abierta de
es una vecindad abierta de
 con respecto a
con respecto a 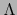 y también con respecto a
y también con respecto a
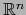 .
En dicho abierto
.
En dicho abierto
 , está bien definida la aplicación
(restringida)
, está bien definida la aplicación
(restringida)
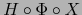 y es diferenciable C.D. en el punto
y es diferenciable C.D. en el punto
 . La restricción de la aplicación
. La restricción de la aplicación
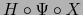 al abierto
al abierto
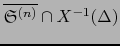 de
de
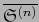 contenido en
contenido en
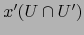 es la misma que la restricción al propio
es la misma que la restricción al propio
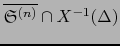 de la aplicación
de la aplicación
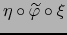 . Así pues,
. Así pues,
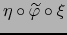 es
diferenciable en el punto
es
diferenciable en el punto  según la definición 4.6.5.
según la definición 4.6.5.
Finalmente de la relación (12) se ve que la aplicación
 es diferenciable en el punto
es diferenciable en el punto  según la definición 4.6.5.
según la definición 4.6.5.

Teorema 5.7
- Sea
 una variedad con borde de clase
una variedad con borde de clase  . La aplicación
idéntica
. La aplicación
idéntica  es diferenciable en todo punto de
es diferenciable en todo punto de  .
.
- Sean
 ,
,  ,
, 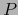 variedades con bordes de clase
variedades con bordes de clase  . Sea
. Sea
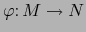 ,
,
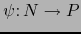 aplicaciones tales que
aplicaciones tales que
 es diferenciable en un punto
es diferenciable en un punto 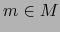 y
y 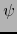 es
diferenciable en el punto
es
diferenciable en el punto
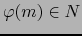 . La aplicación compuesta
. La aplicación compuesta
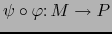 es diferenciable en
es diferenciable en  .
.
Demostración
- Sea
 una variedad con borde de clase
una variedad con borde de clase  . Sean
. Sean  un
punto arbitrario de
un
punto arbitrario de  y
y  un mapa admisible de
un mapa admisible de  en el punto
en el punto
 . La aplicación idéntica
. La aplicación idéntica  leída en el mapa
leída en el mapa
 no es otra que
no es otra que
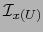 , la aplicación idéntica del
abierto
, la aplicación idéntica del
abierto  de
de
 . Es diferenciable según la definición 4.6.1 en el
punto
. Es diferenciable según la definición 4.6.1 en el
punto  . Luego
. Luego  es diferenciable en el punto
es diferenciable en el punto 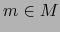 .
.
- Adoptemos las notaciones del enunciado b). Sean
 un mapa
admisible de
un mapa
admisible de  en el punto
en el punto  ,
,  un mapa admisible de
un mapa admisible de  en el
punto
en el
punto 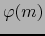 y
y 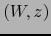 un mapa admisible de
un mapa admisible de 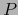 en el punto
en el punto
 . Suponemos que
. Suponemos que
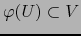 y
y
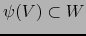 .
La aplicación
.
La aplicación  leída en los mapas
leída en los mapas  y
y  es:
es:
La aplicación 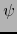 leída en los mapas
leída en los mapas  y
y 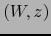 es:
es:
Las hipótesis significan que
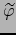 es diferenciable
según la definición 4.6.1 en el punto
es diferenciable
según la definición 4.6.1 en el punto 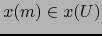 y
y
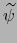 es diferenciable según la definición 4.6.1 en el
punto
es diferenciable según la definición 4.6.1 en el
punto
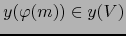 .
.
De ahí se sigue, por el teorema 4.6.5 (``regla de la cadena para
semiespacios cerrados''), que
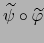 es diferenciable en el punto
es diferenciable en el punto  .
Pero la aplicación
.
Pero la aplicación
 no es otra que
no es otra que
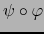 leída en los mapas
leída en los mapas  y
y 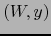 .
.
Luego
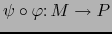 es diferenciable en
es diferenciable en  .
.

Teorema 5.8
Sean  una variedad con borde de clase
una variedad con borde de clase  , de dimensión n y
, de dimensión n y 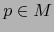 . Sean
. Sean 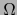 una vecindad de
una vecindad de  en M y
en M y
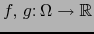 .
.
- Si
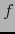 ,
, 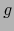 son funciones diferenciables en el punto
son funciones diferenciables en el punto  ,
también
,
también
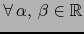 la función
la función
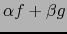 es diferenciable en
es diferenciable en  .
.
- Si
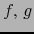 son funciones diferenciables en el punto
son funciones diferenciables en el punto  ,
también la función
,
también la función 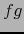 es diferenciable en
es diferenciable en  .
.
- Si
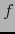 es diferenciable en
es diferenciable en  , satisface
, satisface 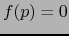 y
y 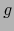 es
continua en
es
continua en  , entonces
, entonces 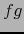 es diferenciable en
es diferenciable en  .
.
Demostración
Sea  un mapa admisible de
un mapa admisible de  en el punto
en el punto  tal que
tal que
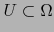 . En
. En 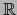 consideramos el mapa admisible
consideramos el mapa admisible
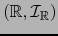 .
.
Las funciones 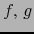 leídas en dichos mapas son respectivamente
leídas en dichos mapas son respectivamente
Empleando la definición 5.5.6 vemos que 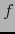 (resp.
(resp. 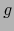 ) es
diferenciable en
) es
diferenciable en  si y sólo si
si y sólo si 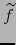 (resp.
(resp.  ) es diferenciable en el punto
) es diferenciable en el punto 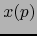 . Vale
. Vale 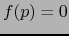 si y sólo si
si y sólo si
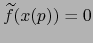 . También claramente
. También claramente 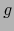 es continua en
es continua en  si
y sólo si
si
y sólo si  es continua en
es continua en 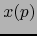 . Debemos, pues, probar
para
. Debemos, pues, probar
para
 definidas en el abierto
definidas en el abierto 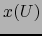 de
de
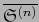 :
:
- Si
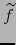 y
y  son diferenciables en
son diferenciables en
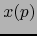 , también
, también
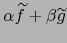 es
diferenciable en
es
diferenciable en 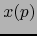 .
.
- Si
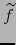 y
y  son diferenciables en el
punto
son diferenciables en el
punto 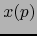 , también
, también
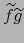 es diferenciable en
es diferenciable en
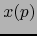 .
.
- Si
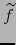 es diferenciable en
es diferenciable en 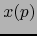 , cumple
, cumple
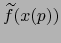 y
y  es continua en
es continua en 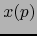 , la
función
, la
función
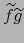 será diferenciable en
será diferenciable en 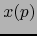 .
.
Pero las afirmaciones a), b), c) siguen sin más del teorema 4.6.4.






Siguiente: Aplicaciones de clase
Arriba: Variedades con borde
Anterior: Producto de una variedad
Guillermo M. Luna
2009-06-14
![]() ,
, ![]() variedades
variedades ![]() con bordes y
con bordes y ![]() una aplicación
una aplicación
![]() . Sean
. Sean ![]() un punto de
un punto de ![]() y
y ![]() una vecindad abierta de
una vecindad abierta de ![]() en
en
![]() .
. ![]() es diferenciable en el punto
es diferenciable en el punto ![]() , si y sólo si la
restricción
, si y sólo si la
restricción ![]() de
de ![]() a la subvariedad abierta
a la subvariedad abierta ![]() de
de
![]() es diferenciable en el punto
es diferenciable en el punto ![]() .
.
![]() mapas admisibles de sendas variedades con bordes
mapas admisibles de sendas variedades con bordes
![]() en sendos puntos
en sendos puntos
![]() tales que
tales que ![]() y
y
![]() .
Decir que
.
Decir que ![]() es diferenciable en
es diferenciable en ![]() significa que:
significa que:
![]() es diferenciable en
es diferenciable en ![]() .
.
![]()
![]() .
Restringimos
.
Restringimos ![]() y
y ![]() a
a
![]() . Por hipótesis
. Por hipótesis
![]() es diferenciable en el punto
es diferenciable en el punto ![]() según la definición 4.6.5.
según la definición 4.6.5.
![]() leída en los mapas
leída en los mapas
![]() es la aplicación:
es la aplicación:
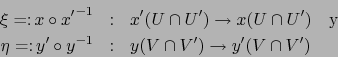
![]() es a fortiori continua en el punto
es a fortiori continua en el punto ![]() y se verifica
y se verifica
![]() . Puesto que
. Puesto que ![]() es una vecindad del punto
es una vecindad del punto
![]() en
en
![]() , por continuidad existe una vecindad abierta
, por continuidad existe una vecindad abierta
![]() de
de ![]() en
en
![]() contenida en
contenida en ![]() tal que
tal que ![]() .
.
![]() , por ser de clase
, por ser de clase ![]() es a fortiori continua en
es a fortiori continua en
![]() . Luego
. Luego
![]() es una vecindad abierta de
es una vecindad abierta de
![]() con respecto a
con respecto a ![]() y también con respecto a
y también con respecto a
![]() .
En dicho abierto
.
En dicho abierto
![]() , está bien definida la aplicación
(restringida)
, está bien definida la aplicación
(restringida)
![]() y es diferenciable C.D. en el punto
y es diferenciable C.D. en el punto
![]() . La restricción de la aplicación
. La restricción de la aplicación
![]() al abierto
al abierto
![]() de
de
![]() contenido en
contenido en
![]() es la misma que la restricción al propio
es la misma que la restricción al propio
![]() de la aplicación
de la aplicación
![]() . Así pues,
. Así pues,
![]() es
diferenciable en el punto
es
diferenciable en el punto ![]() según la definición 4.6.5.
según la definición 4.6.5.
![]() es diferenciable en el punto
es diferenciable en el punto ![]() según la definición 4.6.5.
según la definición 4.6.5.
![]()
![]() es diferenciable en el punto
es diferenciable en el punto ![]() .
Pero la aplicación
.
Pero la aplicación
![]() no es otra que
no es otra que
![]() leída en los mapas
leída en los mapas ![]() y
y ![]() .
.
![]() es diferenciable en
es diferenciable en ![]() .
.
![]()
![]() un mapa admisible de
un mapa admisible de ![]() en el punto
en el punto ![]() tal que
tal que
![]() . En
. En ![]() consideramos el mapa admisible
consideramos el mapa admisible
![]() .
.
![]() leídas en dichos mapas son respectivamente
leídas en dichos mapas son respectivamente