Se llama PERMUTACIÓN de un conjunto a una biyección de éste sobre sí.
![]() designaremos por
designaremos por ![]() el conjunto de todas las permutaciones del intervalo
el conjunto de todas las permutaciones del intervalo ![]() de
de ![]() . Mientras trabajemos con
. Mientras trabajemos con ![]() fijo, los elementos del intervalo
fijo, los elementos del intervalo ![]() , o sea los enteros
, o sea los enteros ![]() los llamaremos D´iGITOS.
los llamaremos D´iGITOS.
La aplicación
![]() de
de
![]() en
en ![]() hace de
hace de ![]() un grupo. Este se llama GRUPO SIMÉTRICO DE GRADO
un grupo. Este se llama GRUPO SIMÉTRICO DE GRADO ![]() . Conforme a una costumbre común escribiremos simplemente
. Conforme a una costumbre común escribiremos simplemente ![]() en vez de
en vez de
![]() . El elemento neutro del grupo
. El elemento neutro del grupo ![]() es la aplicación idéntica de
es la aplicación idéntica de ![]() que designaremos por
que designaremos por ![]() . Si
. Si
![]() , el elemento inverso
, el elemento inverso ![]() de
de ![]() en el grupo
en el grupo ![]() no es otro que la biyección inversa de la biyección
no es otro que la biyección inversa de la biyección ![]() .
.
![]() se verifica:
se verifica:
Demostración
Algo más generalmente, probaremos que si ![]() son conjuntos de cardinalidad
son conjuntos de cardinalidad ![]() , el número de biyecciones de
, el número de biyecciones de ![]() sobre
sobre ![]() es
es ![]() .
La demostración la haremos por inducción sobre
.
La demostración la haremos por inducción sobre ![]() . Para
. Para ![]() la afirmación es trivial. Supongamos
la afirmación es trivial. Supongamos
![]() y el teorema probado para
y el teorema probado para ![]() . Sean
. Sean
![]() e
e
![]() conjuntos de cardinalidad
conjuntos de cardinalidad ![]() .
.
![]() sea
sea ![]() el conjunto de las biyecciones
el conjunto de las biyecciones ![]() de
de ![]() sobre
sobre ![]() tales que
tales que ![]() . La cardinalidad de
. La cardinalidad de ![]() es igual a aquella del conjunto de todas las biyecciones del conjunto
es igual a aquella del conjunto de todas las biyecciones del conjunto
![]() sobre el conjunto
sobre el conjunto ![]() . Por hipótesis de inducción esta cardinalidad es
. Por hipótesis de inducción esta cardinalidad es ![]() . El conjunto de todas las biyecciones de
. El conjunto de todas las biyecciones de ![]() sobre
sobre ![]() es la reunión de los
es la reunión de los ![]() conjuntos
conjuntos ![]() , ajenos a pares, cada uno de cardinalidad
, ajenos a pares, cada uno de cardinalidad ![]() luego tiene cardinalidad
luego tiene cardinalidad
![]() .
.
![]()
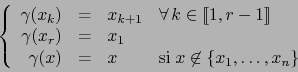
![[*]](footnote.png)
Una condición equivalente reza: Para todo dígito
![]() existe a lo sumo un índice
existe a lo sumo un índice
![]() tal que
tal que
![]() .
.
Demostración
Demostración
Sea dada
![]() .
.
La órbita de un dígito
![]() se reduce a
se reduce a ![]() si y sólo si
si y sólo si ![]() o, como se dice,
o, como se dice, ![]() ``es invariante por
``es invariante por ![]() ''.
''.
Una órbita de ![]() reducida a un sólo punto la llamaremos ´ORBITA TRIVIAL. Puesto que
reducida a un sólo punto la llamaremos ´ORBITA TRIVIAL. Puesto que
![]() ,
, ![]() posee por lo menos una órbita no trivial.
posee por lo menos una órbita no trivial.
Sea
![]() .
. ![]() es un entero
es un entero ![]() .
.
![]() obtenemos por el algoritmo de la división enteros
obtenemos por el algoritmo de la división enteros ![]() y
y ![]() tales que
tales que ![]() y
y
![]() , de donde:
, de donde:
El entero ![]() depende solamente de
depende solamente de ![]() , pues es la cardinalidad de
, pues es la cardinalidad de ![]() . También el ciclo
. También el ciclo
![]() depende solamente de
depende solamente de ![]() pues
pues ![]() es la restricción de
es la restricción de ![]() a
a ![]() :
:
![]() . A su vez
. A su vez
![]() .
.
Si
![]() se verifica:
se verifica:
![\begin{eqnarray*}
&\ & \tau(i)=j \,,\; \tau (j) = i \; \hspace{3em} \mbox{y} \\ ...
...\![ 1,n ]\!] \; \mbox{tal que} \; k \ne i \; \mbox{y} \; k \ne j
\end{eqnarray*}](img404.png)
Demostración
Vale
![]() . Podemos pues suponer ahora
. Podemos pues suponer ahora
![]() . En virtud del teorema 1.2.2 basta probar que
todo ciclo puede representarse como producto de una familia finita de trasposiciones. Esto se sigue de que si
. En virtud del teorema 1.2.2 basta probar que
todo ciclo puede representarse como producto de una familia finita de trasposiciones. Esto se sigue de que si ![]() y si
y si
![]() son dígitos distintos a pares, rige la fórmula:
son dígitos distintos a pares, rige la fórmula:
Advertencia.
La representación de una permutación como producto de trasposiciones está lejos de ser única. P. ej. si ![]() tenemos:
tenemos:
Demostración
En virtud del teorema 1.2.3 basta probar que toda trasposición puede expresarse como producto de trasposiciones de dígitos consecutivos. Consideremos dos dígitos: ![]() y
y ![]() con
con
![]() .
Observamos que la permutación
.
Observamos que la permutación
En el importante teorema que sigue se considera el conjunto de dos elementos ![]() . Podemos mirarlo como p. ej. un subconjunto de
. Podemos mirarlo como p. ej. un subconjunto de ![]() , provisto por la multiplicación inducida por la de
, provisto por la multiplicación inducida por la de ![]() , a saber:
, a saber:
Demostración
Si existe un homomorfismo deseado ![]() , es necesariamente único. En efecto en virtud del teorema 1.2.3 toda permutación
, es necesariamente único. En efecto en virtud del teorema 1.2.3 toda permutación
![]() puede representarse en la forma
puede representarse en la forma
![]() , donde
, donde
![]() son trasposiciones. Por ser
son trasposiciones. Por ser ![]() un homomorfismo vale
un homomorfismo vale
![]() . Además, puesto que
. Además, puesto que ![]() toma el valor
toma el valor ![]() sobre toda trasposición, se sigue de ahí
sobre toda trasposición, se sigue de ahí
![]() . Por tanto se conoce el valor de
. Por tanto se conoce el valor de ![]() sobre toda permutación, elemento de
sobre toda permutación, elemento de ![]() .
.
Probemos la existencia del homomorfismo ![]() . Pongamos:
. Pongamos:
Sean
![]() permutaciones arbitrarias, elementos de
permutaciones arbitrarias, elementos de ![]() . Al escribir (10) con
. Al escribir (10) con ![]() obtenemos
mediante (9), (8) y (10) y otra vez (7)
obtenemos
mediante (9), (8) y (10) y otra vez (7)

Queda por probar que ![]() toma valor
toma valor ![]() sobre toda trasposición. Sea
sobre toda trasposición. Sea
![]() una trasposición arbitraria. Aquí
una trasposición arbitraria. Aquí ![]() son elementos distintos de
son elementos distintos de ![]() . Cabe suponer
. Cabe suponer ![]() y escribir
y escribir ![]() con
con
![]() .
.
Las inversiones de
![]() son:
son:
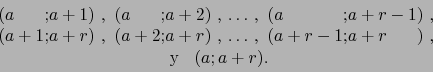
De ahí se sigue:
Si representamos una misma permutación de diferentes maneras como producto de trasposiciones, la paridad del número de factores es siempre la misma o sea depende solamente de ![]() .
.
![]() es una permutación impar si una de las permutaciones
es una permutación impar si una de las permutaciones
![]() es par y la otra es impar.
es par y la otra es impar.
La demostración es inmediata.
Notación.
Se designa por ![]() el conjunto de todas las permutaciones pares de grado
el conjunto de todas las permutaciones pares de grado ![]() .
.
La afirmación se sigue sin más de las implicaciones:
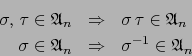
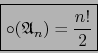
Demostración
Sea ![]() una permutación impar fija de grado
una permutación impar fija de grado ![]() . La aplicación
. La aplicación
![]() es una biyección de
es una biyección de ![]() sobre sí. Intercambia
sobre sí. Intercambia ![]() con su complemento. De ahí la conclusión.
con su complemento. De ahí la conclusión.
![]() Existencia y unicidad del álgebra exterior
Existencia y unicidad del álgebra exterior