Siguiente: Álgebra de Grassmann asociada
Arriba: Elementos de álgebra exterior
Anterior: Elementos de álgebra exterior
Álgebra exterior sobre un espacio vectorial
En el año 1844 el matemático alemán HERMANN GRASSMANN (1809-1877) publicó una obra titulada AUSDEHNUNGSLEHRE (título que aproximadamente traducido al castellano rezaría ``teoría de extensiones''). Una segunda edición ampliada salió a luz en 1848. La obra contiene lo que actualmente llamamos álgebra lineal y también un cálculo geométrico muy eficaz basado en una continuación de ésta, denominada ``álgebra exterior''. Los trabajos de Grassmann fueron de muy lejos adelantados a su época y por tanto mal entendidos. Largo lapso quedaron casi olvidados hasta que en nuestro siglo el gran geómetra francés ELIE CARTAN (1869-1951) hizo del álgebra exterior de Grassmann la base de su propio cálculo de formas diferenciales, instrumento maravilloso en la teoría de variedades diferenciables y, por ende, en todo el análisis global. Gracias a ello el álgebra exterior cobró una posición sólida en la matemática actual y se multiplicaron sus aplicaciones. Inicialmente prolongación de la teoría de espacios vectoriales de dimensión finita, el álgebra exterior no sólo se liberó de la restricción a la dimensión finita, sino que puede exponerse en un marco considerablemente más amplio: aquel de ``módulos". Es parte de una doctrina nombrada ``álgebra multilineal'', más precisamente de un aspecto de ésta, conocido como ``álgebra tensorial''. Aunque esta última desempeña un papel importante en la teoría de variedades diferenciables, no será tratada en nuestro libro elemental. En él nos limitaremos a una exposición sucinta del álgebra exterior sobre un espacio vectorial de dimensión finita, que es todo lo que necesitaremos a continuación. Nuestro afán de brevedad, motivado por el deseo de ganar tiempo y espacio y justificado por el carácter, para nosotros, auxiliar de estos preliminares algebraicos, se pagará desgraciadamente a menudo por algo de artificialidad en la introducción de conceptos.
Subsections





Siguiente: Álgebra de Grassmann asociada
Arriba: Elementos de álgebra exterior
Anterior: Elementos de álgebra exterior
Guillermo M. Luna
2009-06-14
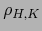
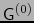 con el cuerpo
con el cuerpo 
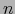 provisto de una
base fija
provisto de una
base fija
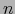 -uplo de vectores con respecto a una base de un espacio vectorial de dimensión
-uplo de vectores con respecto a una base de un espacio vectorial de dimensión