




Siguiente: Aplicaciones multilineales alternadas. Formas
Arriba: Álgebra exterior sobre un
Anterior: Menores de una matriz
Multivectores descomponibles
Partamos de los hechos familiares siguientes:
En esta sección, veremos cómo se pueden generalizar estos hechos a dimensiones mayores que uno, substituyendo vectores no nulos por
multivectores descomponibles no nulos. De este modo, surgirá algo como una ``motivación geométrica'' del álgebra exterior.
En esta sección,  designa un espacio vectorial de dimensión finita sobre un cuerpo conmutativo
designa un espacio vectorial de dimensión finita sobre un cuerpo conmutativo  .
.
Definición 5.1
Sea
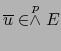 tal que
tal que
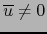 . Definimos:
Patentemente
. Definimos:
Patentemente
 es un subespacio de E.
es un subespacio de E.
Definición 5.2
Sean
 tales que
tales que  . Sean
. Sean
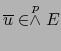 ,
,
 tales que
tales que
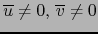 . Se dice que el -VECTOR DIVIDE AL -VECTOR o que
. Se dice que el -VECTOR DIVIDE AL -VECTOR o que  es DIVISIBLE por
es DIVISIBLE por 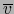 , si existe
, si existe
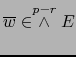 tal que:
tal que:
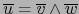 .
.
Teorema 5.1
En todo espacio  de dimensión finita:
de dimensión finita:
- Si
 son multivectores no nulos, rige la implicación:
son multivectores no nulos, rige la implicación:
- Si
 son multivectores no nulos y
son multivectores no nulos y
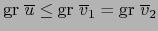 , rige la implicación:
, rige la implicación:
- Si
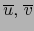 son multivectores no nulos, rige la implicación:
son multivectores no nulos, rige la implicación:
La demostración del teorema 1.5.1 es inmediata.
El teorema fundamental de la sección es:
Teorema 5.2
Sean
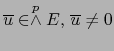 y
y
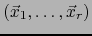 una familia linealmente independiente de vectores de
una familia linealmente independiente de vectores de
 . Vale
. Vale  y
y
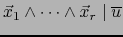 .
.
Demostración
Completamos la familia
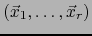 a una base
a una base
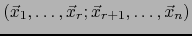 de
de  .
Sea
.
Sea
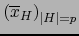 la base de
la base de
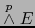 inducida por la precedente. Podemos escribir de manera única:
inducida por la precedente. Podemos escribir de manera única:
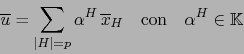 |
(1) |
Sea 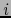 un dígito arbitrario en
un dígito arbitrario en ![$[\![ 1,r ]\!]$](img1094.png) . Por hipótesis,
. Por hipótesis,
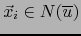 de donde por (1):
de donde por (1):
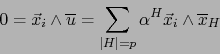 |
(2) |
Pero por el teorema 1.1.6, vale
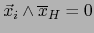 si
si 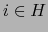 . La relación (2) se reduce pues a:
. La relación (2) se reduce pues a:
o sea:
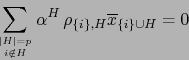 |
(3) |
Ahora bien, los elementos
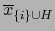 con
con  distintos tales que
distintos tales que 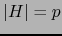 e
e 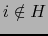 constituyen una parte de la base de
constituyen una parte de la base de
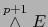 inducida por nuestra base
inducida por nuestra base
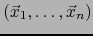 de
de  , luego dichos elementos son linealmente independientes. De la relación (3) se sigue pues la implicación:
, luego dichos elementos son linealmente independientes. De la relación (3) se sigue pues la implicación:
De ahí, por la arbitrariedad del dígito
![$i \in [\![ 1,r ]\!]$](img1135.png) , vemos que de hecho rige la implicación:
, vemos que de hecho rige la implicación:
![\begin{displaymath}
\vert H\vert=p,\; [\![ 1,r ]\!] \not\subset H \, \Rightarrow \, \alpha^H =0
\end{displaymath}](img1136.png) |
(4) |
Ya que supusimos
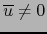 , se sigue de (1) y de (4) que existe
, se sigue de (1) y de (4) que existe
![$H\subset [\![ 1,n]\!]$](img123.png) tal que
tal que 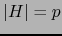 y
y
![$[\![ 1,r ]\!] \subset H$](img1137.png) . Por tanto, necesariamente:
. Por tanto, necesariamente:
También por (4), la relación (1) se reduce a:
![\begin{displaymath}
\overline{u} = \sum_{ \vert H\vert=p \atop [\![ 1,r ]\!] \subset H} \alpha^H \overline{x}_H
\end{displaymath}](img1139.png) |
(5) |
Puesto que la inclusión
![$[\![ 1,r ]\!] \subset H$](img1137.png) implica
implica
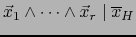 , todos los
términos a la derecha de (5) son divisibles por
, todos los
términos a la derecha de (5) son divisibles por
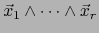 , de ahí que
, de ahí que  es también divisible
por
es también divisible
por
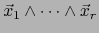 .
.

Corolario 5.1
Si  es un
es un  -vector no nulo, se tiene:
-vector no nulo, se tiene:
Teorema 5.3
Sea
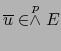 tal que
tal que
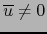 . Se verifica
. Se verifica
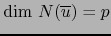 si y sólo si
si y sólo si  es un
es un  -vector descomponible. Al suponer que éste sea el caso, una familia
-vector descomponible. Al suponer que éste sea el caso, una familia
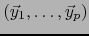 de vectores de
de vectores de  será una base del subespacio
será una base del subespacio
 de
de  si y sólo si existe
si y sólo si existe
 ,
, 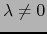 , tal que:
, tal que:
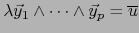 .
.
Demostración
- Supongamos
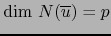 . Sea
. Sea
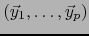 una base del subespacio
una base del subespacio
 . Por el teorema 1.5.2 el
. Por el teorema 1.5.2 el  -vector
-vector
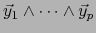 divide a
divide a  , es decir existe
, es decir existe
 ,
, 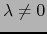 , tal que:
, tal que:
El  -vector
-vector  es, pues, descomponible.
es, pues, descomponible.
- Recíprocamente supongamos que
 es descomponible, o sea, representable en la forma:
es descomponible, o sea, representable en la forma:
En virtud del teorema 1.3.4, nuestra hipótesis
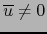 implica que la familia
implica que la familia
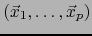 es linealmente independiente. Patentemente
es linealmente independiente. Patentemente
![$\vec{x}_i \land \overline{u} =0 \;\; \forall \, i \in [\![ 1,p]\!]$](img1151.png) , luego los vectores
, luego los vectores
 pertenecen al subespacio
pertenecen al subespacio
 . De ahí :
. De ahí :
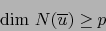 |
(6) |
Pero por el corolario del teorema 1.5.2 vale también:
 |
(7) |
Las relaciones (6) y (7) muestran que
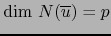 , como afirmamos.
, como afirmamos.
Finalmente, sea
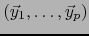 una familia de vectores de
una familia de vectores de  tal que:
tal que:
Ya que
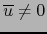 el teorema 1.3.4 implica que la familia
el teorema 1.3.4 implica que la familia
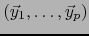 es linealmente independiente. Además,
es linealmente independiente. Además,
![$\vec{y}_i \land \overline{u} =0 \; \forall \, i \in [\![ 1,p ]\!]$](img1156.png) , o sea,
, o sea,
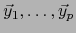 son vectores de
son vectores de
 . La familia
. La familia
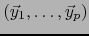 es pues una base del subespacio
es pues una base del subespacio
 de
de  .
.

Teorema 5.4
Sean 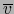 un
un  -vector no nulo y
-vector no nulo y  un
un 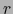 -vector no nulo descomponible sobre
-vector no nulo descomponible sobre  . Se tiene
. Se tiene
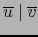 si y sólo si
si y sólo si
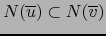 .
.
Demostración
Del teorema 1.5.1 sabemos que, aún sin suponer  descomponible, la relación
descomponible, la relación
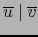 implica
implica
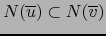 .
Suponiendo
.
Suponiendo  descomponible probemos el recíproco. Tomamos como hipótesis:
descomponible probemos el recíproco. Tomamos como hipótesis:
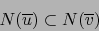 |
(8) |
Podemos escribir:
Por el teorema 1.5.3, de esto se sigue que
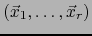 es una base
del subespacio
es una base
del subespacio
 , luego por (8) es una familia linealmente independiente en
, luego por (8) es una familia linealmente independiente en
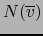 . De ahí, por el teorema 1.5.2:
. De ahí, por el teorema 1.5.2:
 o sea
o sea
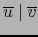 .
.

Teorema 5.5
La aplicación
 del conjunto de todos los multivectores descomponibles no nulos sobre
del conjunto de todos los multivectores descomponibles no nulos sobre  en el conjunto de todos los subespacios de
en el conjunto de todos los subespacios de  es superyectiva. Para multivectores descomponibles no nulos
es superyectiva. Para multivectores descomponibles no nulos
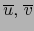 vale
vale
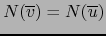 si y sólo si
si y sólo si
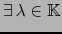 ,
, 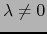 , tal que:
, tal que:
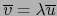 .
.
Demostración
- Sean
 un subespacio de
un subespacio de  y
y
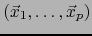 una base de
una base de  . Por el teorema 1.3.4 vale
. Por el teorema 1.3.4 vale
 y, por el teorema 1.5.3:
y, por el teorema 1.5.3:
La aplicación
 es pues superyectiva.
es pues superyectiva.
- Sean
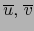 multivectores descomponibles no nulos. Si se verifica
multivectores descomponibles no nulos. Si se verifica
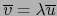 con
con
 ,
, 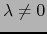 , se tiene patentemente
, se tiene patentemente
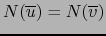 . Recíprocamente, supongamos que vale
. Recíprocamente, supongamos que vale
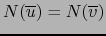 . Por el teorema precedente se sigue:
. Por el teorema precedente se sigue:
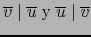 . Así pues,
. Así pues,
 y existe
y existe
 ,
, 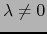 , tal que
, tal que
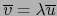 .
.

Teorema 5.6
Sean
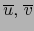 multivectores descomponibles no nulos sobre E. Se tiene:
Se cumple en este caso:
multivectores descomponibles no nulos sobre E. Se tiene:
Se cumple en este caso:
Demostración
- Supongamos que la intersección
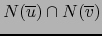 no se reduce a cero. Existe, pues,
no se reduce a cero. Existe, pues, 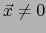 tal que
tal que
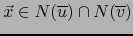 .
Por el teorema 1.5.2 esto implica
.
Por el teorema 1.5.2 esto implica
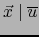 y
y
 . Existen pues multivectores no nulos
. Existen pues multivectores no nulos
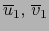 tales que
tales que
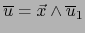 y
y
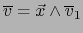 ,
de donde:
,
de donde:
- Supongamos ahora
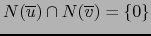 , o sea, la suma
de subespacios
, o sea, la suma
de subespacios
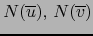 es directa. Escribamos:
es directa. Escribamos:
 ,
,
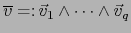 con
con
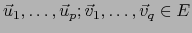 .
.
Por el teorema 1.5.3,
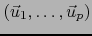 es una base del subespacio
es una base del subespacio
 y
y
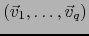 es una base del subespacio
es una base del subespacio
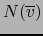 . Por lo sabido de álgebra lineal, se sigue de ahí que la familia
. Por lo sabido de álgebra lineal, se sigue de ahí que la familia
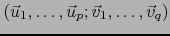 es una base del subespacio
es una base del subespacio
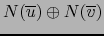 , en particular es linealmente independiente, de donde por el teorema 1.3.4:
, en particular es linealmente independiente, de donde por el teorema 1.3.4:
Finalmente, de nuevo por el teorema 1.5.3:






Siguiente: Aplicaciones multilineales alternadas. Formas
Arriba: Álgebra exterior sobre un
Anterior: Menores de una matriz
Guillermo M. Luna
2009-06-14
![]() designa un espacio vectorial de dimensión finita sobre un cuerpo conmutativo
designa un espacio vectorial de dimensión finita sobre un cuerpo conmutativo ![]() .
.
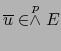 ,
,
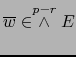 tal que:
tal que:
![]() a una base
a una base
![]() de
de ![]() .
Sea
.
Sea
![]() la base de
la base de
![]() inducida por la precedente. Podemos escribir de manera única:
inducida por la precedente. Podemos escribir de manera única:
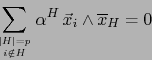
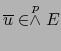 tal que
tal que
![]() una familia de vectores de
una familia de vectores de ![]() tal que:
tal que:
![]() descomponible, la relación
descomponible, la relación
![]() implica
implica
![]() .
Suponiendo
.
Suponiendo ![]() descomponible probemos el recíproco. Tomamos como hipótesis:
descomponible probemos el recíproco. Tomamos como hipótesis:
![]() es una base del subespacio
es una base del subespacio
![]() y
y
![]() es una base del subespacio
es una base del subespacio
![]() . Por lo sabido de álgebra lineal, se sigue de ahí que la familia
. Por lo sabido de álgebra lineal, se sigue de ahí que la familia
![]() es una base del subespacio
es una base del subespacio
![]() , en particular es linealmente independiente, de donde por el teorema 1.3.4:
, en particular es linealmente independiente, de donde por el teorema 1.3.4: