es una aplicación lineal de
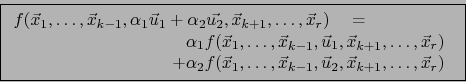
(Una aplicación multilineal es el aspecto más general de ``producto'').
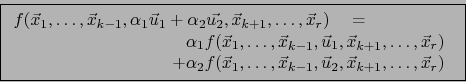
Si ![]() es un conjunto y
es un conjunto y
![]() , designemos por
, designemos por ![]() la POTENCIA CARTESIANA
la POTENCIA CARTESIANA ![]() -ésima de
-ésima de ![]() , vale decir el producto cartesiano
, vale decir el producto cartesiano
![]() , donde
, donde
![]() . Explícitamente
. Explícitamente ![]() es el conjunto de todos los
es el conjunto de todos los
![]() -uplos
-uplos
![]() con
con
![]() .
.
Una aplicación ![]() -lineal alternada
-lineal alternada
![]() se dice una
FORMA -LINEAL ALTERNADA sobre
se dice una
FORMA -LINEAL ALTERNADA sobre ![]() .
.

Demostración
La demostración es esencialmente idéntica a la del teorema 1.15. Por la
comodidad del lector la reproducimos in extenso. Procedemos por inducción sobre el entero ![]() , número mínimo de trasposiciones de dígitos consecutivos cuyo producto es
, número mínimo de trasposiciones de dígitos consecutivos cuyo producto es ![]() .
.
Fijando arbitrariamente
![]() , definimos la aplicación
, definimos la aplicación
![]() por:
por:
Sea
![]() , donde
, donde
![]() son trasposiciones de dígitos consecutivos y
son trasposiciones de dígitos consecutivos y ![]() es el entero mínimo para el cual una tal representación sea posible. Pongamos
es el entero mínimo para el cual una tal representación sea posible. Pongamos
![]() .
. ![]() es el mínimo entero para el cual tal representación de
es el mínimo entero para el cual tal representación de ![]() es posible.
Vale:
es posible.
Vale:
![]() .
.
Definimos
![]() por
por
![]() para
para ![]() . Por el inciso a) se verifica:
. Por el inciso a) se verifica:
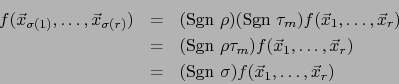
Demostración
Cambiando la numeración si es necesario, podemos suponer que el vector
![]() es una combinación lineal de los vectores
es una combinación lineal de los vectores
![]() , o sea, que se verifica una relación:
, o sea, que se verifica una relación:

Ejemplos de aplicaciones multilineales alternadas
A. Sean ![]() un espacio vectorial de dimensión finita y
un espacio vectorial de dimensión finita y
![]() . La aplicación
. La aplicación
![]() es una aplicación r-lineal alternada de
es una aplicación r-lineal alternada de ![]() en el espacio vectorial
en el espacio vectorial
![]() .
.
B. Sea ![]() un espacio vectorial de dimensión finita n, provisto de una base
un espacio vectorial de dimensión finita n, provisto de una base
![]() . La aplicación:
. La aplicación:
C. Sean ![]() un espacio vectorial de dimensión
un espacio vectorial de dimensión ![]() provisto de una base
provisto de una base
![]() y
y
![]() .
Para todo
.
Para todo ![]() -uplo
-uplo
![]() de vectores en
de vectores en ![]() pongamos:
pongamos:

Afirmamos que la aplicacion de ![]() en
en ![]() :
:
Consideremos, en efecto, el complemento
![]() y los subespacios
y los subespacios
![]() de
de ![]() de sendas bases
de sendas bases
![]() . Se tiene:
. Se tiene:
Escribamos explícitamente
![]() . El menor
. El menor
![]() no es otro que el determinante del
no es otro que el determinante del ![]() -uplo
-uplo
![]() de vectores de
de vectores de ![]() con respecto a la base
con respecto a la base
![]() de
de ![]() . La aplicación (6) puede escribirse, pues, como:
. La aplicación (6) puede escribirse, pues, como:
Sea ![]() un índice arbitrario en
un índice arbitrario en
![]() . Al fijar arbitrariamente
. Al fijar arbitrariamente
![]() ,
,
![]() consideremos la aplicación:
consideremos la aplicación:
Patentemente se anula si dos de los ![]() son iguales.
son iguales.
Por lo tanto (8), o, equivalentemente, (6) es efectivamente una aplicación ![]() -lineal alternada.
-lineal alternada. ![]()
Demostración
En este caso existe un dígito
![]() tal que
tal que
![]() . Luego la columna número
. Luego la columna número ![]() de la matriz
de la matriz
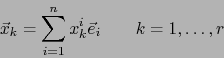
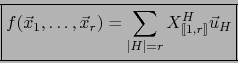
Demostración
Supongamos que existe una aplicación
![]() que cumple las relaciones del inciso a) del enunciado.
que cumple las relaciones del inciso a) del enunciado.
Sea
![]() un
un ![]() -uplo arbitrario de vectores de
-uplo arbitrario de vectores de ![]() .
.
Usando la ![]() -linealidad de
-linealidad de ![]() obtenemos con las notaciones del inciso b) del enunciado:
obtenemos con las notaciones del inciso b) del enunciado:
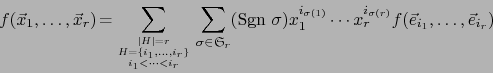
Definimos una aplicación
![]() por la fórmula (12).
En virtud del ejemplo C) citado anteriormente (página
por la fórmula (12).
En virtud del ejemplo C) citado anteriormente (página ![[*]](crossref.png) ):
):
![]() tal que
tal que ![]() la aplicación
la aplicación
![]() es
es ![]() -lineal alternada. De ahí, sin más:
-lineal alternada. De ahí, sin más:
![]() .
Queda por comprobar que si
.
Queda por comprobar que si
![]() ,
,
![]() con
con
![]() vale:
vale:
Nota
En el caso particular ![]() el teorema 2.3 se reduce al siguiente resultado
familiar del álgebra lineal:
el teorema 2.3 se reduce al siguiente resultado
familiar del álgebra lineal:
Si ![]() son espacios vectoriales y
son espacios vectoriales y ![]() es de dimensión finita, provisto
de una base
es de dimensión finita, provisto
de una base
![]() , existe una aplicación
lineal única
, existe una aplicación
lineal única
![]() , tal que
, tal que
![]() son vectores arbitrariamente prescritos de
son vectores arbitrariamente prescritos de ![]() .
.
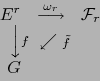
Informalmente hablando, se puede decir que una terna universal
![]() es una máquina que transforma aplicaciones
es una máquina que transforma aplicaciones ![]() -lineales alternadas
-lineales alternadas
![]() en aplicaciones lineales
en aplicaciones lineales
![]() .
.
Se puede también decir que permite obtener todas las aplicaciones ![]() -lineales alternadas
-lineales alternadas ![]() sobre
sobre ![]() a partir de una sola, a saber
a partir de una sola, a saber ![]() , al hacer seguir ésta por una aplicación lineal
, al hacer seguir ésta por una aplicación lineal ![]() conveniente.
conveniente.
Si
![]() es otra terna universal, existe un
único isomorfismo lineal
es otra terna universal, existe un
único isomorfismo lineal ![]() del espacio vectorial
del espacio vectorial ![]() sobre el
espacio vectorial
sobre el
espacio vectorial
![]() tal que:
tal que:
Demostración
Aplicamos la propiedad universal a la terna
![]() al tomar
al tomar
![]() y
y
![]() .
.
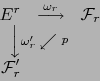
Demostración
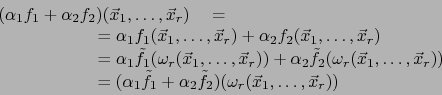
En cuanto a la existencia de una terna universal, la probaremos solamente en
el caso de ser ![]() un espacio vectorial de dimensión finita.
un espacio vectorial de dimensión finita.
Demostración
Debemos probar la propiedad universal (14) para la terna
![]() . Sean
. Sean ![]() un espacio vectorial arbitrario y
un espacio vectorial arbitrario y
![]() .
Se trata de mostrar que existe una única
.
Se trata de mostrar que existe una única
![]() tal que:
tal que:
Sean
![]() vectores arbitrarios en
vectores arbitrarios en ![]() . Escribimos:
. Escribimos:

Por el teorema 1.4.18, tenemos:
Nota
De aquí en adelante (al trabajar con espacios vectoriales de dimensión
finita) nos referiremos a la propiedad universal (14) simplemente como PROPIEDAD UNIVERSAL DE LA -ÉSIMA POTENCIA EXTERIOR DE UN ESPACIO VECTORIAL. En el caso de ser ![]() de dimensión finita, podemos enunciar el teorema 2.5 en la forma siguiente:
de dimensión finita, podemos enunciar el teorema 2.5 en la forma siguiente:
Nota
Mediante la propiedad universal de la terna
![]() se puede
desarrollar la teoría de la
se puede
desarrollar la teoría de la ![]() -ésima potencia exterior de
-ésima potencia exterior de ![]() sin una
teoría previa del álgebra exterior. Evidentemente si uno adopta este
enfoque, queda a su cargo una construcción explícita de
sin una
teoría previa del álgebra exterior. Evidentemente si uno adopta este
enfoque, queda a su cargo una construcción explícita de
![]() .
.
Como consecuencia del teorema 2.1.7, obtenemos sin más:
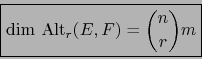

Fijemos una base
![]() de
de ![]() . La aplicación:
. La aplicación:
La aplicación ``determinante de un ![]() -uplo de vectores de
-uplo de vectores de ![]() con respecto a una base de
con respecto a una base de ![]() '' es la única forma
'' es la única forma ![]() -lineal alternada sobre
-lineal alternada sobre ![]() que toma el valor uno sobre dicha base.
que toma el valor uno sobre dicha base.
En un curso elemental de álgebra lineal, en el cual no se desea exponer álgebra exterior, esta propiedad puede servir de punto de partida para una teoría bastante elegante de determinantes. El lector interesado en este asunto didáctico, encontrará una bonita exposición, por ejemplo, en el libro de J. DIXMIER, Matemáticas generales [14].