Sea ![]() un espacio vectorial de dimensión finita provisto de una base
un espacio vectorial de dimensión finita provisto de una base
![]() . Sea
. Sea
![]() la correspondiente base dual de
la correspondiente base dual de ![]() . Sea
. Sea ![]() una aplicación lineal de
una aplicación lineal de ![]() en
en ![]() . Escribimos:
. Escribimos:
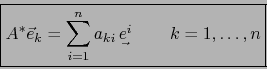
La matriz de ![]() con respecto a las bases
con respecto a las bases
![]() de
de ![]() y
y
![]() de
de ![]() es la traspuesta de la matriz de
es la traspuesta de la matriz de ![]() con respecto
a las mismas bases.
con respecto
a las mismas bases.
Por cierto, este resultado es también una consecuencia inmediata de los teoremas 2.2.7 y 2.2.11.
Como consecuencia de nuestro resultado obtenemos sin más:
A es una aplicación lineal simétrica de ![]() en
en ![]() si y sólo si
si y sólo si
Demostración
En virtud de nuestro último resultado, basta probar que el espacio vectorial
![]() de las matrices simétricas de tipo
de las matrices simétricas de tipo ![]() es de dimensión
es de dimensión
![]() .
.
Ahora bien, una matriz simétrica
![]() de tipo
de tipo ![]() está completamente determinada por sus elementos en la diagonal principal y encima de ésta, o sea, por el sistema
está completamente determinada por sus elementos en la diagonal principal y encima de ésta, o sea, por el sistema
![]() que
consideramos (mediante una ordenación conveniente) como elemento de
que
consideramos (mediante una ordenación conveniente) como elemento de
![]() .
.
El sistema puede prescribirse arbitrariamente. La aplicación que a tal sistema le asigna la correspondiente matriz simétrica de tipo ![]() se puede considerar como un isomorfismo lineal del espacio vectorial
se puede considerar como un isomorfismo lineal del espacio vectorial
![]() sobre el espacio vectorial
sobre el espacio vectorial
![]() . De ahí la conclusión.
. De ahí la conclusión.
![]()
Nota
El teorema 3.1.2 puede considerarse como ``teorema de existencia de aplicaciones lineales simétricas'' pues, en el caso ![]() , garantiza la existencia de aplicaciones lineales simétricas no triviales.
, garantiza la existencia de aplicaciones lineales simétricas no triviales.
Una aplicación
![]() de
de ![]() en
en ![]() se llama PRODUCTO ESCALAR SOBRE
se llama PRODUCTO ESCALAR SOBRE ![]() si:
si:
Nota
Preferimos la terminología ``producto escalar'' a la también muy difundida de ``producto interior'' o ``producto interno''. De hecho, la palabra ``escalar'' se refiere a que nuestra aplicación ``producto'' toma sus valores en el cuerpo ![]() , mientras los adjetivos ``interior'' o ``interno'', de origen histórico, no parecen sugerir gran cosa.
, mientras los adjetivos ``interior'' o ``interno'', de origen histórico, no parecen sugerir gran cosa.
Las notaciones para dicho producto tampoco están unificadas en la literatura. Adoptamos aquella de la escuela BOURBAKI (o de J. DIEUDONNÉ), una costumbre que seguiremos en general en este libro, si acaso no siempre.
![]() se dice una ISOMETR´iA de
se dice una ISOMETR´iA de ![]() en
en ![]() si ``preserva los productos escalares'', es decir, vale:
si ``preserva los productos escalares'', es decir, vale:
Observación
Si
![]() es una isometría de
es una isometría de ![]() en
en ![]() , es una aplicación lineal inyectiva. Luego
si
, es una aplicación lineal inyectiva. Luego
si ![]() es superyectiva, será un isomorfismo lineal de
es superyectiva, será un isomorfismo lineal de ![]() sobre
sobre ![]() . En este caso,
. En este caso, ![]() es
una isometría de
es
una isometría de ![]() sobre
sobre ![]() .
.
Demostración
Supongamos que
![]() es una isometría lineal de
es una isometría lineal de ![]() en
en ![]() . Sea
. Sea ![]() tal que
tal que ![]() .
.
De la relación
![]() , se sigue
, se sigue
![]() .
Por el axioma iii) (lo ``no degenerado'' de un producto escalar), se desprende de ahí
.
Por el axioma iii) (lo ``no degenerado'' de un producto escalar), se desprende de ahí ![]() .
Así pues,
.
Así pues, ![]() es una aplicación lineal inyectiva.
es una aplicación lineal inyectiva. ![]()