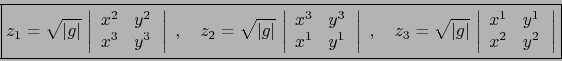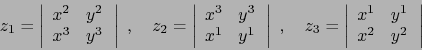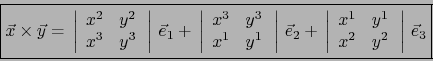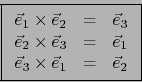Nota
En el caso
![]() se presenta aquí cierta molestia, si se desea orientar
se presenta aquí cierta molestia, si se desea orientar ![]() . Por una parte parece tentador orientar
. Por una parte parece tentador orientar ![]() de suerte que
de suerte que
![]() sea un
elemento de
sea un
elemento de
![]() de sentido positivo. Esto se puede objetar, alegando que la orientación no debe tener que ver con productos escalares, o sea,
con
de sentido positivo. Esto se puede objetar, alegando que la orientación no debe tener que ver con productos escalares, o sea,
con ![]() y que sería más natural tomar como elementos de sentido positivo de
y que sería más natural tomar como elementos de sentido positivo de
![]() aquellos que toman un valor
positivo sobre elementos de sentido positivo de
aquellos que toman un valor
positivo sobre elementos de sentido positivo de
![]() . La fórmula (33) muestra que los dos convenios son opuestos si
. La fórmula (33) muestra que los dos convenios son opuestos si
![]() .
Eludiremos la dificultad no orientando
.
Eludiremos la dificultad no orientando ![]() (por lo menos si
(por lo menos si
![]() ).
).
Observación
Al aplicar el operador ![]() a los dos miembros de (34) obtenemos:
a los dos miembros de (34) obtenemos:
La fórmula (37) hace ver que el ``producto volúmico en ![]() es invariante por
es invariante por ![]() ''.
''.
La fórmula (38) hace ver que el ``producto volúmico en ![]() es invariante por
es invariante por ![]() ''.
''.
Vamos a definir un automorfismo lineal de ![]() que seguiremos designando por
que seguiremos designando por ![]() , transportando sobre
, transportando sobre ![]() , mediante el isomorfismo
, mediante el isomorfismo ![]() , el automorfismo
, el automorfismo ![]() ya conocido de
ya conocido de ![]() .
Formalmente definimos
.
Formalmente definimos
![]() :
:
Claramente el operador ![]() en el primer miembro de (39) es un automorfismo lineal de
en el primer miembro de (39) es un automorfismo lineal de ![]() y
y
![]() transforma (biyectivamente)
transforma (biyectivamente)
![]() en
en
![]() . Más precisamente, su restricción a
. Más precisamente, su restricción a
![]() es:
es:
Podemos también, como alternativa, dar una definición de ![]() en
en ![]() completamente análoga a la definición de
completamente análoga a la definición de ![]() en
en ![]() , a saber:
, a saber:
Demostración
Por la fórmula (39) de arriba, tenemos
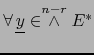
Componentes covariantes y contravariantes de
![]() para
para
![]()
Sea
![]() . Pongamos:
. Pongamos:
De (43) se ve que los elementos ![]() y
y ![]() tienen las mismas componentes
covariantes y las mismas componentes contravariantes.
tienen las mismas componentes
covariantes y las mismas componentes contravariantes.
De (44) se ve que los elementos de
![]() y
y
![]() tienen las mismas
componentes covariantes y las mismas componentes contravariantes.
tienen las mismas
componentes covariantes y las mismas componentes contravariantes.
De esto se desprende que los teoremas 3.3.11 y 3.3.12 enunciados para
![]() , valen
sin cambio para
, valen
sin cambio para
![]() (al reemplazar, bien entendido, las componentes de
(al reemplazar, bien entendido, las componentes de ![]() por las de
por las de ![]() ).
).
Demostración
Los siguientes dos teoremas se demuestran exactamente como sendos teoremas 3.3.14 y 3.3.15.
Terminaremos la exposición teórica de esta sección por dos resultados donde se combinan los operadores
Demostración
El siguiente teorema ofrece una nueva alternativa para definir el operador ![]() en
en ![]() .
.
Demostración
Para terminar la sección trataremos tres ejemplos: los dos primeros serán casos particulares
del último. Los estudiaremos, sin embargo, aparte para facilitar la referencia al lector, pues son
muy elementales y usados.
Ejemplo 3.1. Caso ![]()
Estudiaremos el operador
![]() .
.
![]() , vale por definición:
, vale por definición:

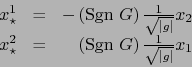
En el caso de ser ![]() un espacio vectorial euclidiano y
un espacio vectorial euclidiano y
![]() una base O.N.P. de
una base O.N.P. de ![]() , las
componentes (a la vez contravariantes y covariantes) de
, las
componentes (a la vez contravariantes y covariantes) de ![]() con respecto a dicha base son
simplemente:
con respecto a dicha base son
simplemente:
(En efecto,
![]() ).
).
Nota
Es algo extraño notar que casi todos los libros elementales de ``cálculo vectorial'', aunque consideran el
siguiente caso ![]() , omiten el estudio anterior del caso
, omiten el estudio anterior del caso ![]() . No obstante ser muy elemental, ese caso
es muy útil en cálculos prácticos.
. No obstante ser muy elemental, ese caso
es muy útil en cálculos prácticos.
Ejemplo 3.2. Caso ![]()
Estudiaremos el operador
![]() . Por el teorema 3.3.10 todo bivector, elemento de
. Por el teorema 3.3.10 todo bivector, elemento de
![]() , es
descomponible.
, es
descomponible.
![]() definimos:
definimos:
Puesto que la aplicación
![]() es una aplicación bilineal de
es una aplicación bilineal de
![]() en
en
![]() y la aplicación
y la aplicación ![]() es una aplicación lineal de
es una aplicación lineal de
![]() en
en ![]() , se ve inmediatamente que:
La aplicación
, se ve inmediatamente que:
La aplicación
![]() es una aplicación bilineal de
es una aplicación bilineal de ![]() en
en ![]() .
.
Hace de ![]() un álgebra en el sentido general de esta palabra, es decir, contrario al convenio al comienzo del §3 del capítulo I. De hecho dicha aplicación
un álgebra en el sentido general de esta palabra, es decir, contrario al convenio al comienzo del §3 del capítulo I. De hecho dicha aplicación
![]() es una aplicación bilineal alternada de
es una aplicación bilineal alternada de ![]() en
en ![]() , pues
la aplicación
, pues
la aplicación
![]() es una aplicación bilineal alternada de
es una aplicación bilineal alternada de ![]() en
en
![]() .
.
Afirmamos que se cumple:
![]() si y sólo si el par
si y sólo si el par
![]() es linealmente dependiente.
es linealmente dependiente.
En efecto, por ser el operador ![]() un isomorfismo de
un isomorfismo de
![]() sobre
sobre ![]() , vale
, vale
![]() si
y sólo si
si
y sólo si
![]() y sabemos que lo último ocurre si y sólo si el
par
y sabemos que lo último ocurre si y sólo si el
par
![]() es linealmente dependiente.
es linealmente dependiente.
Por la definición del operador ![]() :
:
![]() es el único vector de
es el único vector de ![]() que cumple:
que cumple:
La trilinealidad de la aplicación
![]() implica fácilmente en el caso
implica fácilmente en el caso ![]() la regla:
la regla:
Observación
Si
![]() es un par linealmente independiente en
es un par linealmente independiente en ![]() , se tiene:
, se tiene:
Fórmulas
A) Sean
![]() dos pares de vectores de
dos pares de vectores de ![]() . Por el teorema 3.3.15 tenemos:
. Por el teorema 3.3.15 tenemos:
B) Para tres vectores
![]() afirmamos que vale:
afirmamos que vale:
En efecto, por la fórmula (50) (de Cauchy-Binet) obtenemos:

Esta fórmula se obtiene substituyendo en (51)
Observación
Intercambiando los pares
![]() y
y
![]() en (52) obtenemos la identidad:
en (52) obtenemos la identidad:
Advertencia
El producto vectorial no es asociativo.
Sea por ejemplo
![]() una base O.N.P. en un espacio vectorial euclidiano orientado
una base O.N.P. en un espacio vectorial euclidiano orientado ![]() de dimensión 3. Tenemos:
de dimensión 3. Tenemos:
![]() , pues
, pues
![]() , pero por la fórmula del doble producto vectorial:
, pero por la fórmula del doble producto vectorial:
Como ``substituto'' de asociatividad tenemos
![]() :
:
![[*]](footnote.png)
En efecto, por la fórmula del doble producto vectorial se verifican las identidades:

Nota
Álgebras en sentido amplio (no en el sentido restrictivo
del convenio al comienzo del §3 del capítulo I) que satisfacen la identidad de Jacobi, se llaman ´ALGEBRAS DE LIE. Adquirieron una
considerable importancia en la matemática de este siglo.
Un espacio vectorial real de dimensión tres, orientado, de producto escalar, provisto como ``multiplicación'' del producto vectorial,
es un ejemplo de álgebra de Lie.
Expresión analítica
Sea
![]() una base de
una base de ![]() de sentido positivo. Sean
de sentido positivo. Sean
![]() ,
,
![]() vectores
arbitrarios de
vectores
arbitrarios de ![]() . Al efectuar el producto exterior obtenemos:
. Al efectuar el producto exterior obtenemos: