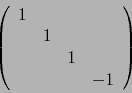Siguiente: El operador de Hodge
Arriba: El operador de Hodge
Anterior: El operador de Hodge
Teorema 3.1
Sean  un espacio de producto escalar de dimensión
un espacio de producto escalar de dimensión  y
y
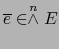 . Si
. Si
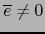 , vale también
, vale también
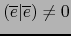 . En otras palabras: No hay un elemento isótropo en
. En otras palabras: No hay un elemento isótropo en
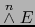 .
.
Demostración
Supongamos
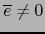 . La familia
. La familia
 reducida al solo elemento
reducida al solo elemento 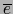 es una base de
es una base de
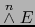 . Todo elemento
. Todo elemento
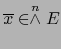 se representa únicamente en la forma
se representa únicamente en la forma
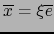 con
con
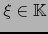 . Si fuese
. Si fuese
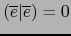 , sería también:
, sería también:
contrariamente al axioma iii) de producto escalar. Esta contradicción establece el teorema.

Demostración
Fijemos
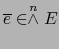 tal que
tal que
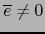 . Todo
. Todo  -vector no nulo de
-vector no nulo de  puede representarse únicamente en la forma
puede representarse únicamente en la forma
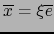 con
con
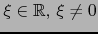 . De
ahí
. De
ahí
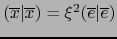 . Ya que aquí
. Ya que aquí 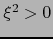 , vemos que
, vemos que
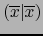 tiene el mismo signo que
tiene el mismo signo que
 .
.

Observación
Si  es un espacio vectorial euclidiano, sabemos del teorema 3.2.4 que también
es un espacio vectorial euclidiano, sabemos del teorema 3.2.4 que también
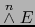 es un espacio vectorial euclidiano, luego en este caso:
es un espacio vectorial euclidiano, luego en este caso:
Observación
Si
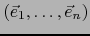 es una base O.N. de
es una base O.N. de  (a suponer que existe), vale:
(a suponer que existe), vale:
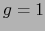 .
.
Teorema 3.3
Con las notaciones de la definición 3.3.1 vale:
Demostración
Por la fórmula (1) del teorema 3.2.1:

El teorema 3.3.3 dice que 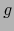 es el gramiano del
es el gramiano del  -uplo
-uplo
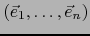 .
.
Corolario 3.1
Si  es un espacio real de producto escalar, provisto de una base
es un espacio real de producto escalar, provisto de una base
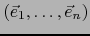 , vale:
, vale:
Demostración
Fijemos arbitrariamente un  -vector no nulo
-vector no nulo 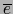 , de sentido positivo. Buscamos un
, de sentido positivo. Buscamos un  -vector
-vector
 con
con 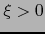 tal que
tal que
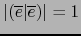 .
Esta condición equivale a:
.
Esta condición equivale a:
de donde la única solución:
Finalmente:
 |
(1) |

Definición 3.2
Una base
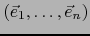 de
de  (necesariamente de sentido positivo) la llamaremos BASE CALIBRADA si:
(necesariamente de sentido positivo) la llamaremos BASE CALIBRADA si:
Teorema 3.5
Si
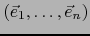 es una base de sentido positivo de
es una base de sentido positivo de  , vale:
, vale:
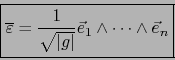 |
(2) |
Dicha base será, pues, una base calibrada si y sólo si:
Demostración
La fórmula (2) se obtiene al tomar
 en la
fórmula (1) del teorema 3.3.4.
en la
fórmula (1) del teorema 3.3.4.

Notación abreviada.
Si  es un espacio vectorial euclidiano, escribiremos abreviadamente BASE O.N.P. por una base ortonormal de sentido positivo de
es un espacio vectorial euclidiano, escribiremos abreviadamente BASE O.N.P. por una base ortonormal de sentido positivo de  .
.
De la observación después de la definición 3.3.1 y del teorema 3.3.5 sigue sin
más:
Corolario 3.2 (del teorema
3.3.5)
En un espacio vectorial euclidiano  toda base O.N.P de
toda base O.N.P de  es una base calibrada de
es una base calibrada de  .
.
Volvemos al caso general de un espacio real, orientado, de producto escalar.
En vista de la definición del producto volúmico, esta fórmula es equivalente a la fórmula (2) del teorema 3.3.5.
Los dos teoremas siguientes son evidentes:
Teorema 3.7
Vale
![$[\vec{x}_1,\ldots \vec{x}_n]=0$](img2322.png) si y sólo si el
si y sólo si el  -uplo
-uplo
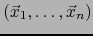 de vectores de
de vectores de  es linealmente dependiente.
es linealmente dependiente.
Teorema 3.8
Supongamos
![$[\vec{x}_1,\ldots,\vec{x}_n] \ne 0$](img2323.png) .
.
Vale
![$[\vec{x}_1,\ldots,\vec{x}_n] >0$](img2324.png) si
si
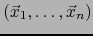 es una base de sentido positivo de E.
es una base de sentido positivo de E.
Vale
![$[\vec{x}_1,\ldots,\vec{x}_n] <0$](img2325.png) si
si
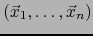 es una base de sentido negativo de E.
es una base de sentido negativo de E.
Esta fórmula equivale a cada una de las siguientes:
De ahí, en presencia de una base de  , el
, el 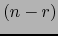 -vector
-vector
 tendrá también las mismas componentes covariantes y las mismas componentes contravariantes que el
tendrá también las mismas componentes covariantes y las mismas componentes contravariantes que el 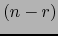 -covector
-covector
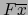 definido
por la fórmula (3).
definido
por la fórmula (3).
Demostración
Tenemos
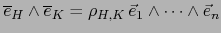 , equivalentemente
al tomar la componente de ambos miembros con respecto al
, equivalentemente
al tomar la componente de ambos miembros con respecto al  -vector patrón
-vector patrón
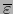 :
:
Al aplicar el teorema 3.3.6 vemos que esto equivale a:
![\begin{displaymath}\mbox{\fbox{${\displaystyle [{\overline e}_H, {\overline e}_K] = \rho_{H,K} \sqrt{\vert g\vert}}$}}
\end{displaymath}](img2343.png) |
(5) |
Puesto que si
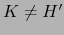 vale
vale
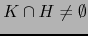 , luego
, luego 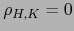 la fórmula (5) es la misma que la del enunciado.
la fórmula (5) es la misma que la del enunciado.

Teorema 3.9
El operador 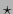 es un isomorfismo lineal de
es un isomorfismo lineal de
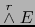 sobre
sobre
 .
.
Demostración
Puesto que
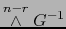 es un isomorfismo lineal de
es un isomorfismo lineal de
 sobre
sobre
 ,
basta probar, en vista de la definición (4), que
,
basta probar, en vista de la definición (4), que  es un isomorfismo lineal de
es un isomorfismo lineal de
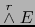 sobre
sobre
 .
.
- Probemos la implicación:
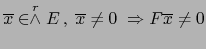 .
.
Sea, pues,
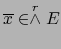 tal que
tal que
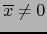 . Usando una base
. Usando una base
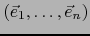 de
de  de sentido positivo escribimos:
de sentido positivo escribimos:
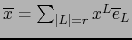 . La hipótesis implica que existe
. La hipótesis implica que existe
![$H\subset [\![ 1,n]\!]$](img123.png) con
con 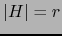 , tal que
, tal que 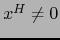 . Por la fórmula (3):
. Por la fórmula (3):
![\begin{displaymath}\mbox{\fbox{${\displaystyle \bigl\langle {\overline e}_{H^\pr...
... L\vert=r} x^L [{\overline e}_L, {\overline e}_{H^\prime}]}$}}
\end{displaymath}](img2352.png) |
(6) |
Por el lema 3.3.1 vale:
La fórmula (6) se reduce, pues, a:
Por lo tanto,
 , como afirmamos.
, como afirmamos.
- Se sigue del inciso a) que
 es una aplicación lineal inyectiva de
es una aplicación lineal inyectiva de
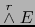 en
en
 . Pero:
. Pero:
probando que  es un isomorfismo de
es un isomorfismo de
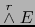 sobre
sobre
 .
.

Corolario 3.3
Consideremos al operador 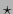 como endomorfismo lineal del álgebra
como endomorfismo lineal del álgebra 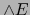 . Con esta óptica
. Con esta óptica 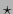 es de hecho un automorfismo lineal del álgebra
es de hecho un automorfismo lineal del álgebra 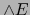 sobre sí.
sobre sí.
Definiciones equivalentes del operador 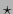
- En virtud de la definición del producto escalar en
 , la fórmula
, la fórmula
dice que
 es el único
es el único 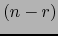 -vector tal que
-vector tal que
 se cumple:
se cumple:
o sea, por la definición (3) de  :
:
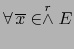 ,
,
 es el único elemento de
es el único elemento de
 tal que:
tal que:
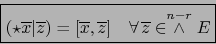 |
(7) |
(Según esta definición, se puede pensar en el operador 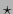 como una ``máquina'' que transforma productos volúmicos en productos escalares).
como una ``máquina'' que transforma productos volúmicos en productos escalares).
- La fórmula (7) puede escribirse equivalentemente
al multiplicar sus dos miembros por el
 -vector patrón
-vector patrón
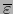 :
:
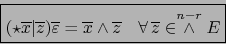 |
(8) |
(Así escrito el operador 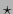 aparece como una máquina que transforma productos exteriores en productos escalares).
aparece como una máquina que transforma productos exteriores en productos escalares).
- Finalmente, para despejar
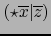 de (8) podemos
escribir esta fórmula de manera equivalente al multiplicar escalarmente sus dos miembros por
de (8) podemos
escribir esta fórmula de manera equivalente al multiplicar escalarmente sus dos miembros por
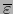 :
:
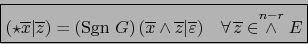 |
(9) |
Casos particulares.
- Caso
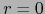 .
.
- Por la fórmula (9) al tomar
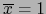 y
y
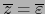 obtenemos:
obtenemos:
y, puesto que
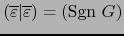 se sigue de ahí:
se sigue de ahí:
o sea,
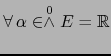 :
:
- Caso
 .
.
- Al tomar en (9):
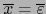 y
y
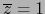 , obtenemos:
, obtenemos:
Destacando:
o sea, para todo elemento
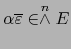 :
:
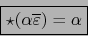 |
(10) |
Observación
Sean
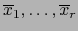 elementos homogéneos del álgebra
elementos homogéneos del álgebra 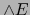 tales que:
tales que:
Por definición del producto volúmico tenemos:
![\begin{displaymath}
{\overline x}_1 \wedge \cdots \wedge {\overline x}_r = [{\overline x}_1, \ldots,{\overline x}_r] {\overline \varepsilon}
\end{displaymath}](img2379.png) |
(11) |
Aplicando el operador (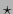 ) a ambos miembros de (11) y usando (10) obtenemos la fórmula:
) a ambos miembros de (11) y usando (10) obtenemos la fórmula:
Nota
La teoría del operador de Hodge la desarrollaremos principalmente mediante cálculo con bases y componentes. Sin repeticiones ulteriores:
Demostración
Por la definición (7) del operador de Hodge tenemos:
y la fórmula deseada resulta como consecuencia inmediata del lema 3.3.1.

Comentario
En vista de la fórmula (25) entre las ``fórmulas analíticas'' después del teorema 3.1.11, el lema 3.3.1 dice:
La componente covariante de índice 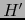 del
del 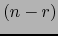 -vector
-vector
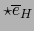 es
es
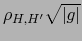 ; las
demás componentes covariantes valen cero. Equivalentemente:
; las
demás componentes covariantes valen cero. Equivalentemente:
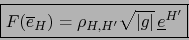 |
(12) |
o sea:
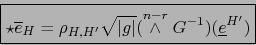 |
(13) |
Vamos a dar una interesante aplicación geométrica de estas fórmulas.
Demostración
Sea 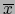 un
un 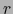 -vector descomponible no nulo. Podemos escribir:
-vector descomponible no nulo. Podemos escribir:
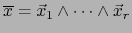 , donde
, donde
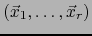 es una familia linealmente independiente de vectores de
es una familia linealmente independiente de vectores de  . Introduzcamos la
notación alternativa:
. Introduzcamos la
notación alternativa:
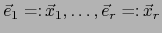 y completemos el
y completemos el 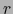 -uplo
-uplo
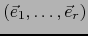 a una base:
a una base:
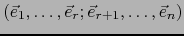 de sentido
positivo. Sea
de sentido
positivo. Sea
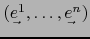 la base de
la base de 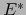 dual de ésta. Por la fórmula (12) del comentario anterior vale:
dual de ésta. Por la fórmula (12) del comentario anterior vale:
 |
(14) |
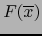 es, pues, un
es, pues, un 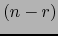 -vector descomponible no nulo.
-vector descomponible no nulo.
También, por la demostración del teorema 2.2.8:
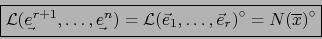 |
(15) |
Ahora bien la fórmula (14) equivale a:
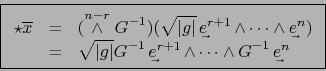 |
(16) |
que es un 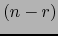 -vector descomponible no nulo. Mediante (16) y (15) :
-vector descomponible no nulo. Mediante (16) y (15) :

Teorema 3.11
(Componentes covariantes de
 en función de las componentes contravariantes de
en función de las componentes contravariantes de 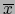 ) Sea
) Sea
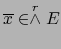 . Escribámoslo
. Escribámoslo
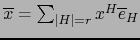 . Designemos por
. Designemos por 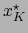 con
con 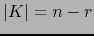 , las componentes covariantes de
, las componentes covariantes de
 . Valen las fórmulas:
. Valen las fórmulas:
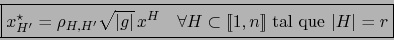 |
(17) |
Demostración
La fórmula (12) del comentario del lema 3.3.2 reza:
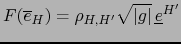 ,
,
Aquí el coeficiente de
 es la componente covariante
es la componente covariante
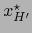 de
de
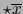 ,
de donde la fórmula (17).
,
de donde la fórmula (17).

Demostración
Sea
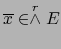 . Por la definición (9) del operador (
. Por la definición (9) del operador ( ) vale:
) vale:
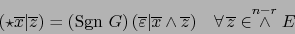 |
(19) |
Por el teorema 3.3.5, se tiene
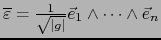 . Luego (19) se convierte en:
. Luego (19) se convierte en:
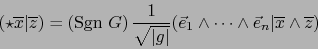 |
(20) |
Aplicando al segundo miembro de (20) la fórmula del teorema 3.2.5, conseguimos:
o sea:
 |
(21) |
donde  son las componentes covariantes de
son las componentes covariantes de 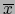 y
y 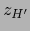 son las
componentes covariantes de
son las
componentes covariantes de 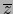 .
.
Pero por la fórmula (28) entre las ``fórmulas analíticas'', después del teorema 3.1.11, tenemos también:
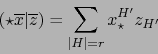 |
(22) |
Finalmente, al igualar los coeficientes de 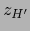 en los segundos miembros de (21) y (22), obtenemos:
en los segundos miembros de (21) y (22), obtenemos:

Teorema 3.13
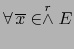 se tiene:
se tiene:
Demostración
Designemos por
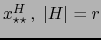 , las componentes contravariantes de
, las componentes contravariantes de
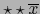 .
Aplicando la fórmula (18) del teorema 3.3.12 con el cambio de
.
Aplicando la fórmula (18) del teorema 3.3.12 con el cambio de 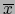 en
en
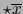 e intercambio de
e intercambio de  con
con  hallamos:
hallamos:
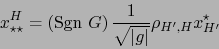 |
(23) |
Por otra parte, por la fórmula (17) del teorema 3.3.11 vale:
 |
(24) |
Llevando (24) a (23) obtenemos:
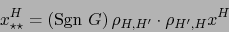 |
(25) |
Pero por el lema 1.1.2 se verifica:
luego, en definitiva, (25) reza:
Esta fórmula es equivalente a la del enunciado.

Observación
Designemos por un momento por 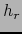 y
y 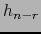 las restricciones del operador
las restricciones del operador  a sendos
espacios vectoriales
a sendos
espacios vectoriales
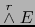 y
y
 . La fórmula del teorema 3.3.13 equivale a:
. La fórmula del teorema 3.3.13 equivale a:
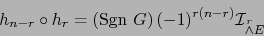 |
(26) |
De ahí, al intercambiar 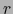 con
con 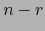 :
:
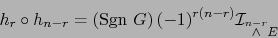 |
(27) |
Las fórmulas (26) y (27) entrañan que 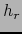 es una biyección de
es una biyección de
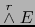 sobre
sobre
 . La biyección
inversa es
. La biyección
inversa es
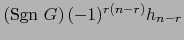 , o sea, ``
, o sea, ``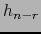 a menos del signo''. Esto ofrece una
nueva prueba del teorema 3.3.9.
a menos del signo''. Esto ofrece una
nueva prueba del teorema 3.3.9.
Teorema 3.14
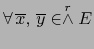 se verifican las fórmulas:
Equivalentemente:
se verifican las fórmulas:
Equivalentemente:
Demostración
En virtud de la simetría del producto escalar basta mostrar que:
Ahora bien, por definición del operador 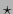 tenemos
tenemos
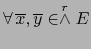 :
:
o sea, por el teorema 3.3.13:
![\begin{displaymath}[\star {\overline y}, {\overline x}]= \left(\mbox{\rm Sgn } G \right)(-1)^{r(n-r)} ({\overline y}\vert {\overline x})
\end{displaymath}](img2438.png) |
(28) |
Pero
![$[\star {\overline y}, {\overline x}] = (-1)^{r(n-r)} [{\overline x}, \star {\overline y}]$](img2439.png) (pues
(pues
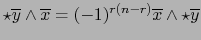 por el teorema 1.1.5). Luego la fórmula (28) se convierte en:
por el teorema 1.1.5). Luego la fórmula (28) se convierte en:

Teorema 3.15
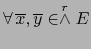 vale:
vale:
Demostración
Por definición del operador 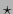 y el teorema 3.3.14 tenemos
y el teorema 3.3.14 tenemos
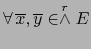 :
:

Informalmente se puede enunciar el teorema 3.3.15 diciendo que el operador 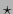 es una ``casi-isometría'' de
es una ``casi-isometría'' de
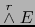 sobre
sobre
 , o sea, una
``isometría a menos del signo''. Será una genuina isometría, si
, o sea, una
``isometría a menos del signo''. Será una genuina isometría, si
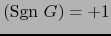 , por ejemplo si
, por ejemplo si  es un espacio vectorial euclidiano. En el caso general,
el teorema 3.3.15 suministra una nueva prueba de que la restricción del operador
es un espacio vectorial euclidiano. En el caso general,
el teorema 3.3.15 suministra una nueva prueba de que la restricción del operador 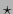 a
a
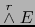 es
una biyección de
es
una biyección de
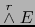 sobre
sobre
 , o sea, una nueva prueba (la tercera) del teorema 3.3.9.
, o sea, una nueva prueba (la tercera) del teorema 3.3.9.
En efecto sea
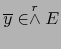 tal que
tal que
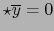 . Del teorema 3.3.15, se sigue de ahí
. Del teorema 3.3.15, se sigue de ahí
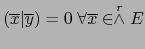 . Por el axioma iii) de productos escalares, esto entraña
. Por el axioma iii) de productos escalares, esto entraña
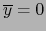 . El operador
. El operador 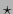 restringido a
restringido a
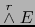 es, pues, inyectivo.
Ya que
es, pues, inyectivo.
Ya que
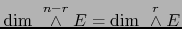 , el operador
, el operador 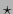 es un isomorfismo lineal de
es un isomorfismo lineal de
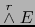 sobre
sobre
 .
.

Corolario 3.4 (del teorema
3.3.15)
Sean
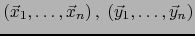 dos
dos  -uplos de vectores de
-uplos de vectores de  . Sabemos que:
de donde, por el teorema 3.3.15:
o sea, en definitiva por el teorema 3.2.1:
Esta fórmula se llama FÓRMULA DE CAUCHY-BINET. Como caso particular obtenemos:
llamada IDENTIDAD DE LAGRANGE.
. Sabemos que:
de donde, por el teorema 3.3.15:
o sea, en definitiva por el teorema 3.2.1:
Esta fórmula se llama FÓRMULA DE CAUCHY-BINET. Como caso particular obtenemos:
llamada IDENTIDAD DE LAGRANGE.
El segundo miembro de la última fórmula es el gramiano del  -uplo
-uplo
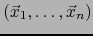 .
.
Una aplicación de la fórmula de Cauchy-Binet: Sean
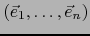 una base de sentido positivo de
una base de sentido positivo de  y
y
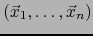 un
un
 -uplo arbitrario de vectores de
-uplo arbitrario de vectores de  .
.
![$\forall \, i,j \in [\![1,n]\!]$](img2455.png) sea
sea
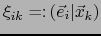 la componente covariante de índice
la componente covariante de índice 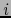 del vector
del vector 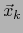 . Vale:
. Vale:
Demostración
Por la fórmula de Cauchy-Binet:
Pero por el teorema 3.3.6,
![$[\vec{e}_1,\ldots,\vec{e}_n]= \sqrt{\vert g\vert}$](img2459.png) , de donde la conclusión.
, de donde la conclusión.

Caracterización geométrica del operador de Hodge (Caso euclidiano).
Si  es un espacio vectorial euclidiano y
es un espacio vectorial euclidiano y 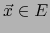 , el número real no negativo,
, el número real no negativo,
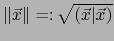 es la
familiar NORMA EUCLIDIANA (para los físicos MAGNITUD) del vector
es la
familiar NORMA EUCLIDIANA (para los físicos MAGNITUD) del vector 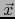 . Si
. Si 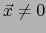 la DIRECCIÓN
de
la DIRECCIÓN
de 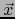 es el subespacio de dimensión uno engendrado por el vector
es el subespacio de dimensión uno engendrado por el vector 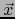 . El SENTIDO del
vector
. El SENTIDO del
vector 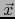 es aquel de los dos sentidos de dicho subespacio
es aquel de los dos sentidos de dicho subespacio
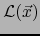 , según la definición después del
teorema 1.4.17, al cual pertenece
, según la definición después del
teorema 1.4.17, al cual pertenece 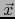 . Sea
. Sea 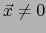 . Supongamos conocida:
. Supongamos conocida:
- la dirección
 del vector
del vector 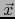 . Aquí
. Aquí
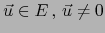 . La información que de
ahí sacamos es que:
. La información que de
ahí sacamos es que:
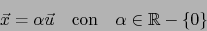 |
(29) |
- Supongamos que además de i) conocemos la ``magnitud'' de
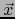 :
:
 .
Este conocimiento suministra:
.
Este conocimiento suministra:
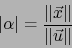 |
(30) |
- Si además de a) y b) conocemos también el sentido de
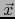 , sabemos que
, sabemos que 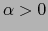 si el sentido de
si el sentido de 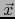 es el de
es el de 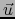 y
y 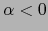 si el sentido de
si el sentido de
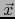 es el de
es el de 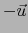 , con lo que, junto con (30), viene determinado el número real
, con lo que, junto con (30), viene determinado el número real 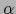 y, luego, por (29) el vector
y, luego, por (29) el vector 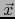 .
.
En resumen: Dirección, magnitud y sentido determinan sin ambigüedad el vector 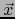 .
.
Volvamos al operador de Hodge.
Sean  un espacio vectorial euclidiano y
un espacio vectorial euclidiano y
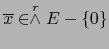 . Puesto que
también
. Puesto que
también
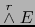 es un espacio vectorial euclidiano, vale
es un espacio vectorial euclidiano, vale
 , pues no
hay elementos isótropos en un espacio vectorial euclidiano. Para caracterizar geométricamente el
, pues no
hay elementos isótropos en un espacio vectorial euclidiano. Para caracterizar geométricamente el 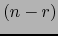 -vector
-vector
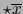 , cabe
suponer que
, cabe
suponer que 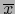 es un
es un 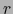 -vector descomponible, pues todo
-vector descomponible, pues todo 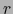 -vector es suma de
-vector es suma de 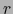 -vectores descomponibles. Por el teorema 3.3.10, sabemos que
también
-vectores descomponibles. Por el teorema 3.3.10, sabemos que
también
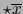 es un
es un 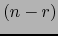 -vector descomponible.
-vector descomponible.
- La ``dirección'' de
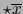 se determina en virtud de los teoremas 3.3.10 y 1.5.5 por la fórmula:
se determina en virtud de los teoremas 3.3.10 y 1.5.5 por la fórmula:
pues si
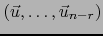 es cualquier base del subespacio
es cualquier base del subespacio
 de
de  , vale:
, vale:
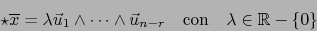 |
(31) |
- Por el teorema 3.3.15, la ``magnitud'' de
 es:
es:
(o sea,
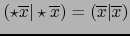 ).
).
- Finalmente, el ``sentido'' de
 viene determinado por la fórmula:
viene determinado por la fórmula:
![\begin{displaymath}\mbox{\fbox{${\displaystyle [{\overline x},\star {\overline x}] >0}$}}
\end{displaymath}](img2476.png) |
(32) |
que sigue del teorema 3.3.14.
En efecto, la fórmula (32) suministra el signo de  en (31).
en (31).
Nota
No sería quizá muy necesario restringir nuestra caracterización geométrica de
 al caso euclidiano. Pero:
al caso euclidiano. Pero:
- Si
 no es un espacio vectorial euclidiano, el método falla en el caso de ser
no es un espacio vectorial euclidiano, el método falla en el caso de ser 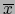 un elemento isótropo de
un elemento isótropo de
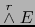 .
.
- La presencia del factor
 quitaría la nitidez y, pienso, carácter intuitivo a los resultados.
quitaría la nitidez y, pienso, carácter intuitivo a los resultados.
Sea dicho de paso, que todos los libros que tratan el operador de Hodge y que conozco, lo hacen solamente
en el caso euclidiano. Como se ve claramente por nuestra exposición, el estudio del caso general no presenta más molestias
que las apariciones del factor
 , donde conviene. Y sí, hay espacios
, donde conviene. Y sí, hay espacios  interesantes a estudiar que
no son euclidianos, por ejemplo, el espacio usado en relatividad restringida es un espacio vectorial real de producto escalar de dimensión 4 que posee bases
con respecto a las cuales
interesantes a estudiar que
no son euclidianos, por ejemplo, el espacio usado en relatividad restringida es un espacio vectorial real de producto escalar de dimensión 4 que posee bases
con respecto a las cuales ![$[G]$](img2478.png) es la matriz diagonal:
es la matriz diagonal:
luego, 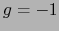 y también
y también
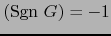 .
.





Siguiente: El operador de Hodge
Arriba: El operador de Hodge
Anterior: El operador de Hodge
Guillermo M. Luna
2009-06-14
![]() . La familia
. La familia
![]() reducida al solo elemento
reducida al solo elemento ![]() es una base de
es una base de
![]() . Todo elemento
. Todo elemento
![]() se representa únicamente en la forma
se representa únicamente en la forma
![]() con
con
![]() . Si fuese
. Si fuese
![]() , sería también:
, sería también:
![]() es el correspondiente isomorfismo simétrico, dicho signo lo designaremos por
es el correspondiente isomorfismo simétrico, dicho signo lo designaremos por
![]() .
.
![]() tal que
tal que
![]() . Todo
. Todo ![]() -vector no nulo de
-vector no nulo de ![]() puede representarse únicamente en la forma
puede representarse únicamente en la forma
![]() con
con
![]() . De
ahí
. De
ahí
![]() . Ya que aquí
. Ya que aquí ![]() , vemos que
, vemos que
![]() tiene el mismo signo que
tiene el mismo signo que
![]() .
.
![]()
![]() es un espacio vectorial euclidiano, sabemos del teorema 3.2.4 que también
es un espacio vectorial euclidiano, sabemos del teorema 3.2.4 que también
![]() es un espacio vectorial euclidiano, luego en este caso:
es un espacio vectorial euclidiano, luego en este caso:
![]() es una base O.N. de
es una base O.N. de ![]() (a suponer que existe), vale:
(a suponer que existe), vale:
![]() .
.
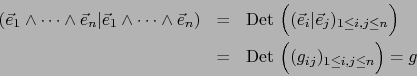
![]() es el gramiano del
es el gramiano del ![]() -uplo
-uplo
![]() .
.

![]() -vector no nulo
-vector no nulo ![]() , de sentido positivo. Buscamos un
, de sentido positivo. Buscamos un ![]() -vector
-vector
![]() con
con ![]() tal que
tal que
![]() .
Esta condición equivale a:
.
Esta condición equivale a:
![]() es un espacio vectorial euclidiano, escribiremos abreviadamente BASE O.N.P. por una base ortonormal de sentido positivo de
es un espacio vectorial euclidiano, escribiremos abreviadamente BASE O.N.P. por una base ortonormal de sentido positivo de ![]() .
.
![]() se dice PRODUCTO AREOLAR en vez de producto volúmico.
se dice PRODUCTO AREOLAR en vez de producto volúmico.
![]() y los correspondientes grados
y los correspondientes grados
![]() , fijados, la aplicación
, fijados, la aplicación
![]() es una aplicación
es una aplicación ![]() -lineal del espacio
-lineal del espacio
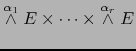 en
en ![]() .
.
![]() de
de ![]() en
en ![]() es una forma
es una forma ![]() -lineal alternada sobre
-lineal alternada sobre ![]() .
.
![]() no es otro que el determinante del
no es otro que el determinante del ![]() -uplo
-uplo
![]() de vectores de
de vectores de ![]() con respecto a cualquier base calibrada de
con respecto a cualquier base calibrada de ![]() .
.
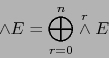
![]() . Sea
. Sea ![]() un elemento arbitrario de
un elemento arbitrario de
![]() . La aplicación
. La aplicación
![]() de
de
![]() en
en ![]() es una forma lineal
sobre
es una forma lineal
sobre
![]() , elemento de
, elemento de
![]() . Designémosla por
. Designémosla por
 . Vale pues:
. Vale pues:
![]() por la fórmula:
por la fórmula:
![]() , equivalentemente
al tomar la componente de ambos miembros con respecto al
, equivalentemente
al tomar la componente de ambos miembros con respecto al ![]() -vector patrón
-vector patrón
![]() :
:
![]() tal que
tal que
![]() . Usando una base
. Usando una base
![]() de
de ![]() de sentido positivo escribimos:
de sentido positivo escribimos:
![]() . La hipótesis implica que existe
. La hipótesis implica que existe
![]() con
con ![]() , tal que
, tal que ![]() . Por la fórmula (3):
. Por la fórmula (3):
![\begin{displaymath}[{\overline e}_L, {\overline e}_{H^\prime}]=
\left\{
\begin{a...
... \sqrt {\vert g\vert} & \mbox{si}\; L=H \\
\end{array}\right.
\end{displaymath}](img2353.png)
![]()
 se cumple:
se cumple:
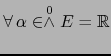 :
:
![]() elementos homogéneos del álgebra
elementos homogéneos del álgebra ![]() tales que:
tales que:

![]() del
del ![]() -vector
-vector
![]() es
es
![]() ; las
demás componentes covariantes valen cero. Equivalentemente:
; las
demás componentes covariantes valen cero. Equivalentemente:
![]() un
un ![]() -vector descomponible no nulo. Podemos escribir:
-vector descomponible no nulo. Podemos escribir:
![]() , donde
, donde
![]() es una familia linealmente independiente de vectores de
es una familia linealmente independiente de vectores de ![]() . Introduzcamos la
notación alternativa:
. Introduzcamos la
notación alternativa:
![]() y completemos el
y completemos el ![]() -uplo
-uplo
![]() a una base:
a una base:
![]() de sentido
positivo. Sea
de sentido
positivo. Sea
![]() la base de
la base de ![]() dual de ésta. Por la fórmula (12) del comentario anterior vale:
dual de ésta. Por la fórmula (12) del comentario anterior vale:
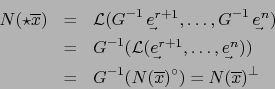
 . Valen las fórmulas:
. Valen las fórmulas:
![]() ,
,
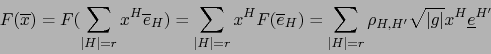
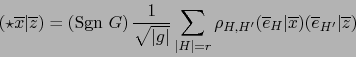
![]() , las componentes contravariantes de
, las componentes contravariantes de
![]() .
Aplicando la fórmula (18) del teorema 3.3.12 con el cambio de
.
Aplicando la fórmula (18) del teorema 3.3.12 con el cambio de ![]() en
en
![]() e intercambio de
e intercambio de ![]() con
con ![]() hallamos:
hallamos:
![]() y
y ![]() las restricciones del operador
las restricciones del operador ![]() a sendos
espacios vectoriales
a sendos
espacios vectoriales
![]() y
y
![]() . La fórmula del teorema 3.3.13 equivale a:
. La fórmula del teorema 3.3.13 equivale a:
![]() es una ``casi-isometría'' de
es una ``casi-isometría'' de
![]() sobre
sobre
![]() , o sea, una
``isometría a menos del signo''. Será una genuina isometría, si
, o sea, una
``isometría a menos del signo''. Será una genuina isometría, si
![]() , por ejemplo si
, por ejemplo si ![]() es un espacio vectorial euclidiano. En el caso general,
el teorema 3.3.15 suministra una nueva prueba de que la restricción del operador
es un espacio vectorial euclidiano. En el caso general,
el teorema 3.3.15 suministra una nueva prueba de que la restricción del operador ![]() a
a
![]() es
una biyección de
es
una biyección de
![]() sobre
sobre
![]() , o sea, una nueva prueba (la tercera) del teorema 3.3.9.
, o sea, una nueva prueba (la tercera) del teorema 3.3.9.
![]() tal que
tal que
![]() . Del teorema 3.3.15, se sigue de ahí
. Del teorema 3.3.15, se sigue de ahí
![]() . Por el axioma iii) de productos escalares, esto entraña
. Por el axioma iii) de productos escalares, esto entraña
![]() . El operador
. El operador ![]() restringido a
restringido a
![]() es, pues, inyectivo.
Ya que
es, pues, inyectivo.
Ya que
![]() , el operador
, el operador ![]() es un isomorfismo lineal de
es un isomorfismo lineal de
![]() sobre
sobre
![]() .
.
![]()
![\begin{eqnarray*}
{[\vec{x}_1,\ldots,\vec{x}_n]} &=& \star (\vec{x}_1 \wedge \cd...
...,\vec{y}_n]} &=& \star(\vec{y}_1 \wedge \cdots \wedge \vec{y}_n)
\end{eqnarray*}](img2451.png)
![]() una base de sentido positivo de
una base de sentido positivo de ![]() y
y
![]() un
un
![]() -uplo arbitrario de vectores de
-uplo arbitrario de vectores de ![]() .
.
![]() sea
sea
![]() la componente covariante de índice
la componente covariante de índice ![]() del vector
del vector ![]() . Vale:
. Vale:
![\begin{eqnarray*}
\mbox{\rm Det }\left( (\xi_{ik})_{1\le i,k \le n} \right) &=& ...
... \right)[\vec{e}_1,\ldots,\vec{e}_n][\vec{x}_1,\ldots,\vec{x}_n]
\end{eqnarray*}](img2458.png)
![]() es un espacio vectorial euclidiano y
es un espacio vectorial euclidiano y ![]() , el número real no negativo,
, el número real no negativo,
![]() es la
familiar NORMA EUCLIDIANA (para los físicos MAGNITUD) del vector
es la
familiar NORMA EUCLIDIANA (para los físicos MAGNITUD) del vector ![]() . Si
. Si ![]() la DIRECCIÓN
de
la DIRECCIÓN
de ![]() es el subespacio de dimensión uno engendrado por el vector
es el subespacio de dimensión uno engendrado por el vector ![]() . El SENTIDO del
vector
. El SENTIDO del
vector ![]() es aquel de los dos sentidos de dicho subespacio
es aquel de los dos sentidos de dicho subespacio
![]() , según la definición después del
teorema 1.4.17, al cual pertenece
, según la definición después del
teorema 1.4.17, al cual pertenece ![]() . Sea
. Sea ![]() . Supongamos conocida:
. Supongamos conocida:
![]() un espacio vectorial euclidiano y
un espacio vectorial euclidiano y
![]() . Puesto que
también
. Puesto que
también
![]() es un espacio vectorial euclidiano, vale
es un espacio vectorial euclidiano, vale
![]() , pues no
hay elementos isótropos en un espacio vectorial euclidiano. Para caracterizar geométricamente el
, pues no
hay elementos isótropos en un espacio vectorial euclidiano. Para caracterizar geométricamente el ![]() -vector
-vector
![]() , cabe
suponer que
, cabe
suponer que ![]() es un
es un ![]() -vector descomponible, pues todo
-vector descomponible, pues todo ![]() -vector es suma de
-vector es suma de ![]() -vectores descomponibles. Por el teorema 3.3.10, sabemos que
también
-vectores descomponibles. Por el teorema 3.3.10, sabemos que
también
![]() es un
es un ![]() -vector descomponible.
-vector descomponible.
![]() al caso euclidiano. Pero:
al caso euclidiano. Pero: