Siguiente: El jacobiano Arriba: Preliminares geométricos y de Anterior: La funcional

Más sobre diferenciales

Aquellos teoremas que serán citados en esta sección sin demostraciones son clásicos. El lector podrá encontrar las demostraciones completas, por ejemplo, en uno de los libros [4,8,13,33].

Sea ${\displaystyle {\cal E} \supset {\cal S} \mathop{\longrightarrow}\limits_{\varphi} {\cal F}}$. Suponemos que el espacio afín normado $\cal F$ es de dimensión finita y provisto de un referencial $(J; \vec{f}_1,\ldots,\vec{f}_m)$. $\forall \, p \in {\cal S}$ ponemos:

$$\fbox{${\displaystyle \varphi (p) =J + \sum_{i=1}^m \varphi^i (p) \vec{f}_i}$}$$

Las funciones $\varphi^1,\ldots,\varphi^m \colon {\cal S} \to {\mathbb{R}}$ se llaman las FUNCIONES COORDENADAS DE CON RESPECTO AL REFERENCIAL $(J; \vec{f}_1,\ldots,\vec{f}_m)$ del espacio afín normado $\cal F$.

Teorema 4.1   Sea a un punto interior de $\cal S$.

1. Sea $\vec u \in E$. Existe la derivada $\partial_{\vec u} \varphi(a)$ según el vector $\vec u$ de $\varphi$ en el punto a si y sólo si existen las derivadas $\partial_{\vec u} \varphi^i (a)$ para $i=1,\ldots,m$ y entonces:
   
   $$\fbox{${\displaystyle \partial_{\vec u}\varphi (a)= \sum_{i=1}^m \partial_{\vec u}\varphi^i (a) \vec{f}_i}$}$$
   
   

2. La aplicación $\varphi$ es diferenciable en el punto $a$, si y sólo si las funciones $\varphi^1,\ldots, \varphi^m$ son diferenciables en $a$ y entonces $\forall \, \vec u \in E$:
   
   $$\fbox{${\displaystyle d\varphi (a) \vec u= \sum_{i=1}^m \langle \vec u , d\varphi^i (a) \rangle \vec{f}_i}$}$$
   
   

Teorema 4.2 (y definición)   Sean ${\cal E},\, \cal F$ espacios afines normados de dimensiones finitas sobre sendos espacios vectoriales $E, F$, provistos de sendos referenciales $(I;\vec{e}_1,\ldots,\vec{e}_n)$, $(J; \vec{f}_1,\ldots,\vec{f}_m)$. Se supone: ${\cal E} \supset {\cal S} \mathop{\longrightarrow}\limits_{\varphi} {\cal F}$ y que $\varphi$ es diferenciable en un punto interior $a$ de $\cal S$. Esto implica por la observación 2 después del teorema 4.3.1 que $\forall \, \vec u \in E$ existe la derivada $\partial_{\vec u} \varphi(a)$. En particular existen $\partial_k \varphi (a),\; k=1,\ldots,n$ las derivadas parciales de $\varphi$ en $a$ con respecto a la base $(\vec{e}_1,\ldots,\vec{e}_n)$ de $E$. Luego por el teorema 4.4.1 existen las $mn$ derivadas parciales $\partial_k \varphi^i (a) \;i=1,\ldots,m;\;k=1,\ldots,n$. La matriz $m \times n$: $\left( \partial_k \varphi^i (a) \right)_{1 \le k \le n}^{1 \le i \le m}$ es la matriz de la diferencial $d\varphi (a)$ con respecto a las bases $(\vec{e}_1,\ldots,\vec{e}_n)$ de E y $(\vec{f}_1,\ldots,\vec{f}_m)$ de $F$. Se llama la MATRIZ JACOBIANA DE LA APLICACIÓN $\varphi$ en el punto $a$ con respecto a los referenciales considerados.

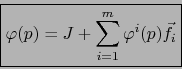
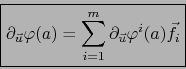
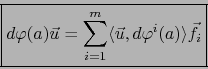
En el caso particular ${\cal E}=E = {\mathbb{R}}^n,\, {\cal F}=F = {\mathbb{R}}^m$ se usa generalmente los referenciales $(0;\vec{e}_1,\ldots,\vec{e}_n),\,(0;\vec{f}_1,\ldots,\vec{f}_m)$ donde $(\vec{e}_1,\ldots,\vec{e}_n)$, $(\vec{f}_1,\ldots,\vec{f}_m)$ son las bases naturales de ${\mathbb{R}}^n$ y ${\mathbb{R}}^m$ respectivamente.

Siguiente: El jacobiano Arriba: Preliminares geométricos y de Anterior: La funcional