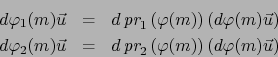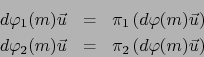abreviadamente
Sea ![]() un punto interior de
un punto interior de ![]() . La aplicación
. La aplicación
![]() es diferenciable en el
punto
es diferenciable en el
punto ![]() si y sólo si las aplicaciones
si y sólo si las aplicaciones
![]() y
y
![]() son
diferenciables en el punto
son
diferenciables en el punto ![]() . En este caso se cumple
. En este caso se cumple
![]() :
:
Abreviadamente:
Sea ![]() un punto interior de
un punto interior de ![]() . La aplicación
. La aplicación
![]() es diferenciable en el
punto
es diferenciable en el
punto ![]() si y sólo si las aplicaciones
si y sólo si las aplicaciones
![]() y
y
![]() son
diferenciables en el punto
son
diferenciables en el punto ![]() . En este caso se cumple
. En este caso se cumple
![]() :
:
Demostración
Asimismo
![]() es una aplicación afín y
es una aplicación afín y
![]() .
.
De topología general se sabe que
![]() y
y
![]() son aplicaciones continuas. Del teorema 4.3.4 se sigue
que
son aplicaciones continuas. Del teorema 4.3.4 se sigue
que
![]() y
y
![]() son aplicaciones diferenciables en
son aplicaciones diferenciables en
![]() y
y
![]() y
y
![]()