Todo punto ![]() posee una vecindad abierta
posee una vecindad abierta ![]() contenida en
contenida en ![]() tal que:
tal que:
Demostración
Sean ![]() ,
, ![]() los espacios vectoriales asociados con sendos espacios afines
los espacios vectoriales asociados con sendos espacios afines
![]() .
.
Sean
![]() una base de
una base de ![]() y
y
![]() un referencial
de
un referencial
de ![]() . Sean
. Sean
![]() , las funciones coordenadas de
, las funciones coordenadas de
![]() con respecto a dicho referencial. Sea
con respecto a dicho referencial. Sea ![]() . La matriz de la aplicación lineal
. La matriz de la aplicación lineal
![]() con respecto a las bases
con respecto a las bases
![]() de
de ![]() y
y
![]() de
de ![]() es la matriz jacobiana
es la matriz jacobiana
Sea
![]() . Por la ``consecuencia'' del teorema 1.4.19, la matriz (1) posee un menor no nulo de orden
. Por la ``consecuencia'' del teorema 1.4.19, la matriz (1) posee un menor no nulo de orden ![]() , mientras todos sus menores de órdenes mayores que
, mientras todos sus menores de órdenes mayores que ![]() son
nulos. Cambiando, si es necesario, la numeración tanto de los
son
nulos. Cambiando, si es necesario, la numeración tanto de los ![]() como de los
como de los ![]() podemos
suponer que
podemos
suponer que
De esto y de (2) se sigue que existe una vecindad abierta ![]() de
de ![]() contenida en
contenida en ![]() tal que:
tal que:
Advertencia
Es posible que se tenga
![]() , para todo
, para todo ![]() tal que
tal que
![]() .
.
Sea, por ejemplo,
![]() la aplicación:
la aplicación:
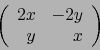
Si ![]() es inmersión (resp. sumersión) en un punto
es inmersión (resp. sumersión) en un punto ![]() , existe
una vecindad abierta
, existe
una vecindad abierta ![]() de
de ![]() contenida en
contenida en ![]() tal que
tal que ![]() es inmersión (resp. sumersión) en
es inmersión (resp. sumersión) en
![]() , vale decir
, vale decir
![]() (resp.
(resp.
![]() ,
,
![]() ).
).
Nota
Salvo los casos mencionados en el teorema 4.5.13, es una circunstancia muy excepcional que el rango de una
aplicación sea constante en toda una vecindad de un punto.
Terminaremos citando, de nuevo sin demostración, una importante consecuencia del teorema 4.5.10. Desempeñará un papel
esencial en el capítulo 8.
Este resultado generaliza el primer enunciado en el teorema 4.5.11.
Demostración
Sean ![]() un abierto de
un abierto de ![]() y
y ![]() un punto arbitrario de
un punto arbitrario de ![]() . Aplicamos el teorema del
rango constante con
. Aplicamos el teorema del
rango constante con ![]() en vez de
en vez de ![]() ,
, ![]() en vez de
en vez de ![]() y
y ![]() . Por dicho
teorema existen una vecindad abierta
. Por dicho
teorema existen una vecindad abierta ![]() de
de ![]() contenida en
contenida en ![]() , una vecindad abierta
, una vecindad abierta ![]() de
de ![]() en
en ![]() tal que
tal que
![]() , isomorfismos
, isomorfismos ![]() :
: ![]() de
de ![]() sobre
sobre ![]() ,
, ![]() de
de ![]() sobre
sobre ![]() tales que:
tales que: